Лекция 1.
- §2. Понятие функции комплексной
переменной.
- 1. Множество задания функции
комплексной переменной - понятие области комплексной переменной.
- 2. Множество значений функции
комплексной переменной. Отображение g-D.
- 3. Однолистность функции комплексной
переменной.
- 4. Задание f(z)=u(x,y)+iv(x,y)-
одновременное задание двух функций действительной переменной в области
g.
Пусть на комплексной
плоскости задано множество E и закон, ставящий " zО E в соответствие определенное комплексное число w: z w, тогда говорят, что на E
задана функция комплексной
переменной f(z)=w. E-множество
задания (z);
w, тогда говорят, что на E
задана функция комплексной
переменной f(z)=w. E-множество
задания (z);
Множество M - значений
соответствующих w- множество значений f(z). Задание f(z) есть задание
соответствия (отображения) E M.
M.
Примеры. а) w=az+b (поворот,
растяжение и параллельный перенос),
б)w=zn, в) w=1/z (симметричное отражение относительно
вещественной оси, инверсия).
Структура
множеств E и M может быть весьма разнообразной. Мы будем рассматривать случаи,
когда E и M- области на комплексной плоскости.
Понятие области комплексной плоскости - это то же самое,
что и понятие области плоскости (x,y).
Определение.Областью g комплексной плоскости Z называется
множество точек этой плоскости, удовлетворяющее условиям:
1)Все zО g являются внутренними
точками g.
2)Любые
z1, z2 О g можно соединить ломаной с конечным числом звеньев,
состоящих только из zО g.
Примеры. а) |z|<1 - область; б) |z|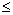 1-не область; в) {z: |z|<1}И {z: |z-5i|<1} не
область;
1-не область; в) {z: |z|<1}И {z: |z-5i|<1} не
область;
Напомним понятие
внутренней точки.
Определение. Точка z0
называется внутренней точкой множества g, если $ e
-окрестность точки z0 : пz-z0п<e все точки которой
принадлежат g.
Примеры. а) z=0 - внутренняя точка множества
|z|<1; б) z=i - не является внутренней точкой множества |z|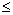 1.
1.
Таким образом, в определении области условие
1) означает, что g- открытое множество.
2)
означает, что g- связное множество.
Итак, область- открытое связное множество.
Определение.Точка z0 называется граничной точкой множества g,
если в " ее
e -окрестности
имеются как zО g,
так и zП g.
Примеры. а) z=0 - граничная точка множества
|z|>0; б) z=i - граничная точка множества |z|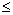 1.
1.
Совокупность граничных
точек области g называется
границей области g. (обозначения: 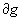 , C, G , S и т.д.)
, C, G , S и т.д.)
Граница множества может состоять из конечного числа
точек, и даже из одной точки (как, например, у множества |z|>0).
Определение. Замыкание области g, состоящее в присоединении к g ее
границы g называется
замкнутой областью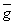 =g+
=g+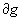 .
.
Множество |z|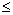 1 - замкнутое.
1 - замкнутое.
На расширенной
комплексной плоскости (т.е. комплексной плоскости с бесконечно удаленной точкой замкнутое множество называется компактным.
Итак, будем рассматривать случай, когда w=f(z) задана в g
и отображает g на область D комплексной плоскости w.
Отображение однозначно (по определению.
Если z1, z2 О g и z1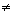 z2 :
f(z1)=w1
z2 :
f(z1)=w1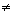 w2= f(z2), то
отображение взаимно однозначно
w2= f(z2), то
отображение взаимно однозначно
g<=>D.
В этом случае g называется
областью однолистности f(z) и f(z) называется
однолистной в g.
Примеры. а) w=const, w=az+b -однозначные и
однолистные; б) w=zn , w=ez- однозначные, но не однолистные; в) w=Ln z╨ |z|+i Arg(z), w= - не однозначный функции.
- не однозначный функции.
При g<=> D в D
$ обратная
функция z=j
(w), осуществляющая отображение D g.
g.
Если
отображение g D
однозначно, но не однолистно, то можно говорить об обратной функции, но она не
будет однозначной. Об этом позже.
D
однозначно, но не однолистно, то можно говорить об обратной функции, но она не
будет однозначной. Об этом позже.
При z=x+iy,
f(z)=w=u+iv=u(x,y)+iv(x,y). Тем самым задание f(z) в g комплексной плоскости z
есть одновременное задание двух действительных функций двух действительных
переменных в области g плоскости (x,y). Поэтому свойства функций комплексной
переменной во многом определяются свойствами функции двух действительных
переменных.