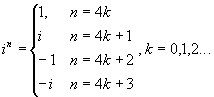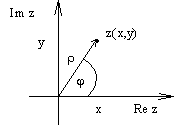Лекция.1.
 1.
Комплексные числа и последовательности комплексных чисел.
1.
Комплексные числа и последовательности комплексных чисел.
п.1. Понятие
комплексного числа. Геометрическая интерпретация.
Определение. Комплексным
числом называется пара действительных чисел с установленным
порядком следования чисел z=(a,b), a=Re z, b=Im z. Действительные числа
включаются в множество комплексных чисел. a=(a,0)-вещественное число, (0,b)-чисто
мнимое число. (0,1)=i- мнимая единица. Еще примеры комплексных чисел: 0=(0,0),
-1=(-1,0), -i=(0,-1).
Комплексные числа можно изображать точками на комплексной плоскости.
I. Действия с комплексными числами.
1) Равенство. Два комплексных
числа равны, если равны их действительные и мнимые части: z1=(a1,b1),
z2=(a2,b2).
Если z1=z2 Ы a1=a2,
b1=b2.Операция сравнения
не
определена. Множество комплексных чисел- неупорядоченное множество.
2) Сложение. z1+z2=(a1+a2,b1+
b2).
Пример: (0,1)+(1,0)=(1,1).
3) Умножение. z1·z2=(a1
a2-b1
b2, a1b2+a2b1).
Операции сложения и умножения включают
действия с действительными числами.
Пример: Умножение чисто вещественного
числа на чисто мнимое число. (b,0)x(0,1)=(0,b)= ib -тем самым чисто мнимое
число есть произведение соответствующего действительного числа на мнимую
единицу.Ю
алгебраическая форма записи комплексного числа z=a+ib=Re z+i Im z.
Обратные операции.
4) Вычитание. z1-z2=(a1-a2,b1-
b2).
5) Деление.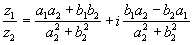 .
Пример.
1/i = -i.
.
Пример.
1/i = -i.
6) Возведение в целую степень. Действия
с многочленами.
Примеры: a) i2=i
i=(0,1)(0,1)=-1. б) 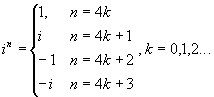
в) z=(a,b)=a+ib. z2=(a+ib)2=a2+2iab-b2=(a2-b2)+i2ab
=> Re z2=(a2- b2), Im z2=2ab.
7) Комплексное сопряжение.
z=(a, b)=a+ib; Re z= a, Im z=b;
z*= (a,-b)=a-ib. Re z*=a ; Im z*=
-b. => Re z =(z+z*)/2; Im z =(z-z*)/2i.
Некоторые свойства. (z1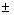 z2)*=
z1*
z2)*=
z1*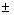 z2*;
(z1z2)*= z1*z2*;(z1/z2)*=
z1*/z2*; (z*)*=z.
z2*;
(z1z2)*= z1*z2*;(z1/z2)*=
z1*/z2*; (z*)*=z.
Примеры. а) z z*=(a+ib)(a-ib)=a2+b2;
б) (z z) *=(z2)*= (a2- b2)-i2ab;
в) z1/z2= z1 z2*/
z2 z2*.
г) i*=-i; 1*=1.
II. Геометрическая интерпретация комплексных
чисел.
| z=(x,y)=x+iy <=> точка плоскости (x,y).
Взаимно однозначное соответствие. Комплексная
плоскость.
Ось абсцисс Imz=0- действительная ось.
Ось ординат Re z=0- мнимая ось.
|
|
Простейшие множества точек на комплексной
плоскости.
Примеры. а) |z-z0|=a
(a>0) - окружность с центром в точке z0
радиуса a;
б) |z-z0|<a
(a>0) - открытый круг с центром в точке z0
радиуса a;
в) |z-z0|>a
(a>0) - внешность открытого круг с центром в точке z0
радиуса a;
г) a<|z-z0|<b
(0<a<b) - открытое кольцо с центром в точке z0
;
д) arg(z-z0)= j
- луч, с началом в точке z0,
идущий под углом j
к положительному направлению действительной оси.
е) a
<arg(z-z0)<b
- внутренность неограниченного открытого сектора с вершиной в точке z0
и
углом раскрыва b -a
.
ж) Re z= a - прямая, || мнимой оси, проходящая
через точку (a,0);
з) Im z= b - прямая, || действительной
оси, проходящая через точку (0,b);
Тригонометрическая и показательная формы
записи комплексного числа
Полярные координаты (x,y) <=>
(r ,j
), где x=.r cos j
, y=r sin j ,
r =(x2+y2)1/2=п
zп =((Re z)2+(Im z)2)1/2-
модуль комплексного числа,
tg j =y/x. j
=j0+2p
k- аргумент комплексного числа.
Arg z=arg z+2p k, 0 arg z
arg z  2p
.
2p
.
Для комплексного числа 0=(0,0) модуль
равен 0, а аргумент не определен.
Тригонометрическая форма записи комплексного
числа: z=r (cosj
+isinj )=r eij-
(формула Эйлера)-
показательная форма записи комплексного числа.
Примеры. а)|z|2=z
z*=a2+b2.; z2 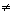 |z|2;
|z|2;
б)z=1: |1|=1, arg 1=0; 1=1(cos 0 +i sin
0)= 1ei0;
в) z=i: |i|=1, arg i=p
/2; i=1(cos p /2 +i sin p
/2)= 1eip /2;
г) z=-1: |-1|=1, arg (-1)= p
; -1=1(cos p +i sin p
)= 1eip ;
д) z=-i: |-i|=1, arg (-i)= 3p
/2; -i=1(cos 3p /2 +i sin 3p
/2)= 1ei3p /2;
e) z=1+i: |1+i|=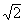 , arg (1+i)=
p
/4; 1+i=
, arg (1+i)=
p
/4; 1+i=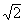 (cos p
/4 +i sin p /4)=
(cos p
/4 +i sin p /4)= 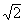 eip
/4;
eip
/4;
ж) z=eij;
|eij |=1, arg (eij)=
j
; eij=1 (cos j
+i sin j );
з) z=-eij;
|-eij |=1, arg (-eij)=
p
+j ; -eij=1
(cos(p +j ) +i sin(p
+j ))=ei(p +j
)
Геометрическая интерпретация сложения
и умножения.
Сложение двух комплексных чисел
можно рассматривать как сложение двух векторов на плоскости. При этом справедливы
Неравенства треугольника пz1+z2п пz1п+пz2п;
пz1-z2п
пz1п+пz2п;
пz1-z2п пz1п-пz2п
пz1п-пz2п
пz1-z2п-
расстояние между z1 и z2
на комплексной плоскости.
e -окрестность
точки z0: пz-z0п<e,
0<пz-z0п<e
- выколотая (проколотая)
e -окрестность
точки z0.
При умножении двух комплексных
чисел их модули перемножаются (растяжение или сжатие), а
аргументы
складываются (поворот на плоскости). z1=a1+i
b1=r 1eia;
z2=a2+i b2=r2eib;
z1 z2=r1r2ei(a
+b ) => |z1z2|=|z1||z2|;
arg(z1 z2)=arg z1+ arg z2 .
При делении двух комплексных чисел
их модули делятся (модуль знаменателя ╧
0), а аргументы вычитаются: z1/z2=(r1/r2)ei(a
-b ) => z1/z2|=|z1|/|z2|;
arg(z1/z2)=arg z1- arg z2
.
Алгебраической формой записи комплексных
чисел удобно пользоваться при операциях сложения и вычитания, а показательной-
при умножении, делении, возведении в целую степень, извлечении целого корня
(возведение в рациональную степень).
Возведение в целую степень.
zn=[r (cosj
+isinj )]n=[r
eij ]=rneinj=
=r n(cos(nj
)+isin(nj )); Формула
Муавра: (cosj +isinj
)n = cos(nj )+isin(nj
).
Пример: (1+i)3=(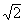 eip
/4)3=23/2 ei3p
/4=23/2(cos(3p /4)+i sin(3p
/4))=-2+2i ;
eip
/4)3=23/2 ei3p
/4=23/2(cos(3p /4)+i sin(3p
/4))=-2+2i ;
Извлечение целого корня (возведение
в рациональную степень).
z=r eij=
r
ei(j +2p k)
, k=0,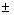 1,
1,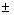 2... .
2... . 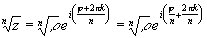 =>
корень n-той степени из комплексного числа имеет n различных значений,
котторые получаются при k=0, 1, 2...n-1.
=>
корень n-той степени из комплексного числа имеет n различных значений,
котторые получаются при k=0, 1, 2...n-1.
Пример: 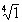 =1
ei(0+2p k)/4={1 (k=0), i (k=1), -1
(k=2), -i (k=3) }.
=1
ei(0+2p k)/4={1 (k=0), i (k=1), -1
(k=2), -i (k=3) }.
П.2. Последовательности
комплексных чисел.
Определение "Последовательностью
комплексных чисел называют упорядоченное счетное множество комплексных
чисел."
Члены последовательности (элементы) располагаются в порядке следования
их номеров. Обозначение: {zn}.
Сходящиеся последовательности.
Определение. "Комплексное
число z называется пределом последовательности {zn},
если для " e
>0 $ N(e ): п
zn-zп <e
для " n N."
N."
Обозначения: {zn} z;
z; 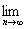 zn=z.
zn=z.
Примеры. а) 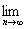 (1+z/n)n=ez, (z=x+iy);
б)
(1+z/n)n=ez, (z=x+iy);
б) 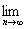 arg[(-1)n/n]
не $ , т.к
arg[(-1)n/n]=0 при четных
n, а при нечетных n arg[(-1)n/n]=p
.
arg[(-1)n/n]
не $ , т.к
arg[(-1)n/n]=0 при четных
n, а при нечетных n arg[(-1)n/n]=p
.
Каждый член последовательности zn=an+ibn
: {zn}={an}+i{bn}-
одновременное задание двух действительных последовательностей.
Теорема 1.1.
"Необходимым и достаточным условием сходимости
{zn} z= a+ib является требование {an}
z= a+ib является требование {an} a; {bn}
a; {bn} b."
b."
Доказательство.
Необходимость. "e>0
$
N(e ): пzn-zп<e
для " n N
Юпan-aп
N
Юпan-aп пzn-zп<e
,
пzn-zп<e
,
пbn-bп пzn-zп
<e Ю {an}
пzn-zп
<e Ю {an} a, {bn}
a, {bn} b.
b.
Достаточность. "e
>0 $ N1(e
): пan-aп
<e /2 для "
n N1,
$
N2(e):
пbn-bп<e/2
для " n
N1,
$
N2(e):
пbn-bп<e/2
для " n N2ЮN=max{N1,N2}:
пzn-zп
N2ЮN=max{N1,N2}:
пzn-zп пan-aп+пbn-bп<e
для " n
пan-aп+пbn-bп<e
для " n N.
n
N.
n
Определение. Последовательность
{zn} называется ограниченной,
если $
A: " n пznп<A.
Любая сходящаяся последовательность ограничена.
Теорема 1.2. Из всякой ограниченной
последовательности можно выделить сходящуюся подпоследовательность.
Доказательство. Основано на Теореме
1*) и соответствующем
свойстве сходящихся ограниченных последовательностей вещественных чисел
(Теорема Больцано-Вейерштрасса *).
Поскольку {zn}ограничена,
то соответствующие ей действительные последовательности {an}
и {bn} также ограничены
(пanп,пbnп пan+i
bnп =(an2+bn2)1/2=пznп<A
для " n).
пan+i
bnп =(an2+bn2)1/2=пznп<A
для " n).
Т.к. пanп<A
Ю$
{ank} a:
пaп<A.
Последовательности {ank}
соответствует {bnk}: пbnkп<AЮ$
{bnl}
a:
пaп<A.
Последовательности {ank}
соответствует {bnk}: пbnkп<AЮ$
{bnl} b, причем {anl}
b, причем {anl} a Ю (по Теореме1
*)
{znl}
a Ю (по Теореме1
*)
{znl} z=a+ib:
пzп<A.
n
z=a+ib:
пzп<A.
n
Критерий Коши. "Необходимым
и достаточным условием сходимости {zn} z является требование, чтобы для " e
>0 $ N(e ): пzn+m-znп<e
для
" n
z является требование, чтобы для " e
>0 $ N(e ): пzn+m-znп<e
для
" n N и " m>0.
N и " m>0.
Доказательство.
Основано на Теореме1 *)
и критерии Коши *)для
последовательности действительных чисел.
Необходимость. Т.к. последовательность
{zn} (zn= an+i bn)
сходится, то сходятся и действительные последовательности. Ю
для " e
>0 и " m>0 $
N1(e):
пan+m-anп<e/2
для и $ N2(e):
для " n N2(e).Ю$
N(e)= max{N1,N2}:
пzn+m-znп<e
для
" n>N(e)
(в силу неравенства треугольника *).
N2(e).Ю$
N(e)= max{N1,N2}:
пzn+m-znп<e
для
" n>N(e)
(в силу неравенства треугольника *).
Достаточность.
Из того, что пzn+m-znп<e
для
Ю пan+m-anп,
пbn+m-bnп пzn+m-znп<e
, что является достаточными условиями сходимости {an}
и {bn}, т.е {zn}-сходится.
n
пzn+m-znп<e
, что является достаточными условиями сходимости {an}
и {bn}, т.е {zn}-сходится.
n
Неограниченно возрастающие последовательности
.Если для "
A>0 $ N(A):
пznп>A
для " n>N(A),
то последовательность {zn}
называется неограниченно возрастающей.
Примеры. а) zn=zn
при |z|>1; б) zn= i n.
В обычном смысле они не сходятся, но оказывается
удобным считать, что
$ z =
= ;
; 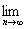 zn=
zn= . Единственная бесконечно удаленная
точка комплексной плоскости. Все неограниченно возрастающие последовательности
сходятся к этой единственной точке. Если {zn}
неограниченно возрастающая, то {xn=1/zn}
. Единственная бесконечно удаленная
точка комплексной плоскости. Все неограниченно возрастающие последовательности
сходятся к этой единственной точке. Если {zn}
неограниченно возрастающая, то {xn=1/zn} 0. Отсюда легко получить правила арифметических действий с бесконечно удаленной
точкой: 1/
0. Отсюда легко получить правила арифметических действий с бесконечно удаленной
точкой: 1/ =0,. 1/0=
=0,. 1/0= , z·
, z· =
= , z
, z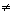 0, z+
0, z+ =
= , z/
, z/ =0,
=0,
z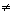
 . Операции 0/0 и
. Операции 0/0 и  /
/ являются неопределенными .
являются неопределенными .
 2.
Понятие функции комплексной переменной.
2.
Понятие функции комплексной переменной.
Пусть на комплексной
плоскости задано множество E и закон, ставящий "
zО E в соответствие
определенное комплексное число w: z w, тогда говорят, что на E задана функция
комплексной переменной f(z)=w. E-множество
задания (z);
w, тогда говорят, что на E задана функция
комплексной переменной f(z)=w. E-множество
задания (z);
Множество M - значений соответствующих
w- множество значений f(z). Задание f(z) есть задание соответствия
(отображения) E M.
M.
Примеры. а) w=az+b (поворот,
растяжение и параллельный перенос),
б)w=zn, в) w=1/z (симметричное
отражение относительно вещественной оси, инверсия).
Структура множеств E и M может быть весьма
разнообразной. Мы будем рассматривать случаи, когда E и M- области на комплексной
плоскости.
Понятие области комплексной плоскости
- это то же самое, что и понятие области плоскости (x,y).
Определение.Областью
g комплексной плоскости Z называется множество точек этой плоскости, удовлетворяющее
условиям:
1)Все zО
g являются внутренними *)
точками g.
2)Любые z1,
z2 О
g можно соединить ломаной с конечным числом звеньев, состоящих только из
zО g.
Примеры. а) |z|<1 - область;
б) |z| 1-не область; в) {z: |z|<1}И
{z: |z-5i|<1} не область;
1-не область; в) {z: |z|<1}И
{z: |z-5i|<1} не область;
Напомним понятие внутренней
точки.
Определение.
Точка z0 называется внутренней
точкой множества g, если $ e
-окрестность точки z0 : пz-z0п<e
все
точки которой принадлежат g.
Примеры. а) z=0 - внутренняя точка множества |z|<1; б) z=i
- не является внутренней точкой множества |z| 1.
1.
Таким образом, в определении области условие
1) означает, что g- открытое*)
множество.
2) означает, что g- связное
множество.
Итак, область-
открытое *)
связное *)
множество.
Определение.Точка
z0 называется граничной
точкой множества g, если в "
ее e -окрестности
имеются как zО
g, так и zП g.
Примеры. а) z=0 - граничная точка
множества |z|>0; б) z=i - граничная точка множества |z| 1.
1.
Совокупность граничных
*)
точек области g называется границей области
g. (обозначения:  ,
C, G , S
и т.д.)
,
C, G , S
и т.д.)
Граница множества может состоять из конечного
числа точек, и даже из одной точки (как, например, у множества |z|>0).
Определение. Замыкание
области g, состоящее в присоединении к g ее границы ╤
g называется замкнутой областью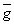 =g+
=g+ .
.
Множество |z| 1 - замкнутое.
1 - замкнутое.
На расширенной
комплексной плоскости (т.е. комплексной плоскости с бесконечно удаленной
точкой *)замкнутое
множество *)
называется компактным.
Итак, будем рассматривать случай, когда
w=f(z) задана в g и отображает g на область D комплексной плоскости w.
Отображение однозначно
(по определению*).
Если z1,
z2 О
g и z1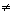 z2
: f(z1)=w1
z2
: f(z1)=w1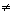 w2=
f(z2), то отображение взаимно
однозначно
w2=
f(z2), то отображение взаимно
однозначно
g<=>D.
В этом случае g
называется областью однолистности f(z) и f(z) называется
однолистной
в g.
Примеры. а) w=const, w=az+b -однозначные
и однолистные; б) w=zn , w=ez-
однозначные, но не однолистные; в) w=Ln z╨
|z|+i Arg(z), w=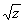 -
не однозначный функции.
-
не однозначный функции.
При g<=>
D в D $ обратная
функция z=j
(w), осуществляющая отображение D g.
g.
Если отображение g D
однозначно, но не однолистно, то можно говорить об обратной функции, но
она не будет однозначной. Об этом позже.
D
однозначно, но не однолистно, то можно говорить об обратной функции, но
она не будет однозначной. Об этом позже.
При z=x+iy,
f(z)=w=u+iv=u(x,y)+iv(x,y). Тем самым задание f(z) в g комплексной плоскости
z есть одновременное задание двух действительных функций двух действительных
переменных в области g плоскости (x,y). Поэтому свойства функций комплексной
переменной во многом определяются свойствами функции двух действительных
переменных.
 3.
Непрерывность функции комплексной переменной.
3.
Непрерывность функции комплексной переменной.
п1. Понятие предела
(предельного значения) функции комплексной переменной в точке z0Оg.
Определение 1. (по Гейне)Комплексное
число w0 называется пределомf(z),
zО g, в точке z0Оg,
если для " {zn} z0 соответствующая последовательность
{f(zn)}
z0 соответствующая последовательность
{f(zn)} w0.
w0.
Замечание. Предполагается,
что z0 является точкой сгущения
(предельной точкой *)
множества g.
Определение.Точка
z0О g
называется точкой сгущения (предельной точкой) множества
g, если в " e
- окрестности точки z0 содержатся
точки множества g, отличные от z0.
Определение 2. (по Коши)Комплексное
число w0 называется пределомf(z),
zО g, в точке z0Оg,
если для "e >0 $d
(e ,z0)>0 : | f(z)-w0
|<e , как только
0<| z-z0|<d
Обозначение: 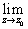 f(z)=
w0.
f(z)=
w0.
Замечание. Это определение
имеет смысл лишь при конечных значениях z0
и w0 в отличие от определения
предела по Гейне *).
Определения по Гейне и по Коши эквивалентны,
что легко доказать самим.
Доказательство.
1) 2 1 (Коши
1 (Коши Гейне). Пусть
f(z) удовлетворяет 2. Возьмем "e
>0 и выберем соответствующее d (e
)>0. Рассмотрим произвольную последовательность {zn}
Гейне). Пусть
f(z) удовлетворяет 2. Возьмем "e
>0 и выберем соответствующее d (e
)>0. Рассмотрим произвольную последовательность {zn} z0 и найдем N[d
(e )]=N(e
): для " n
z0 и найдем N[d
(e )]=N(e
): для " n N(e ) 0<|zn-z0|<d
. Тогда по условию 2. 0<|f(zn)-w0|<e
для
" n
N(e ) 0<|zn-z0|<d
. Тогда по условию 2. 0<|f(zn)-w0|<e
для
" n N(e). А т.к. e
>0- любое и {zn}
N(e). А т.к. e
>0- любое и {zn} z0-произвольная,
то это значит, что {f(zn)}
z0-произвольная,
то это значит, что {f(zn)} w0,
т.е. выполнено 1.
w0,
т.е. выполнено 1.
2) 1 2 (Гейне
2 (Гейне Коши). Предположим
противное: пусть верно1, а 2- неверно.
Коши). Предположим
противное: пусть верно1, а 2- неверно.
Это значит, что
$e0>0,
что "d n>0
$
znОg,
что при 0<|zn-z0 |<dn
, будет выполнено |f(z)-w0|>e0.
Выберем {dn} 0 и соответствующую ей последовательность {zn},
удовлетворяющую предыдущим неравенствам. Тогда получим, что $
{zn}
0 и соответствующую ей последовательность {zn},
удовлетворяющую предыдущим неравенствам. Тогда получим, что $
{zn} z0,
а {f(zn)}не
z0,
а {f(zn)}не  w0. Т.е. 1.- неверно. Получили
противоречие. Сделанное предположение неверно. Т.е. из 1
w0. Т.е. 1.- неверно. Получили
противоречие. Сделанное предположение неверно. Т.е. из 1 2. n
2. n
п2. Непрерывность функции.
Определение непрерывности f(z) в точке
z0. Функция
комплексной переменной f(z), zО
g, называется непрерывной в
точке z0О g,
если $ ограниченный
предел :
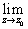 f(z)= w0
и w0= f(z0),
т.е.
f(z)= w0
и w0= f(z0),
т.е. 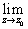 f(z)=
f(z0).
f(z)=
f(z0).
Очевидно, при этом достаточно малая d
- окрестность точки z0 отображается
f(z) на достаточно малую e
- окрестность точки w0= f(z0).
Определение непрерывности функции в
точке в терминах e -d
.Функция комплексной
переменной f(z), zО
g, называется непрерывной в
точке z0О g,
если
" e >0 $d
(e ,z0)>0
: для " z : |z-z0|<d
; |f(z)-f(z0)| <e .
Замечание 1. Это определение
распространяется как на внутренние *),
так и на граничные *)
точки множества.
Определение.Точка
z0 называется изолированной
точкой множества g, если в $
такая ее e
-окрестность, в которой нет других точек множества g.
Замечание 2. По определению функция
считается непрерывной в изолированной *)
точке z0О g.
Замечание 3. Понятие непрерывности
функции f(z), zО
g, в точке z0О g
справедливо и в случае бесконечно удаленной точки z0= *).
*).
При этом под пределом функции f(z) при
z
 по Гейне *)
надо понимать предел последовательности {f(zn)},
где {zn}- "
неограниченно возрастающая последовательность *).
по Гейне *)
надо понимать предел последовательности {f(zn)},
где {zn}- "
неограниченно возрастающая последовательность *).
В e
-d определении
непрерывности функции f(z) при z
 *)
условие ╫ z-z0╫<d
надо заменить на условие |z| >R.
*)
условие ╫ z-z0╫<d
надо заменить на условие |z| >R.
Примеры: а) функции w=az+b,
w=z*, w=const, w=Re z, w=zn,
w=|z| - являются непрерывными на всей комплексной плоскости.
б) функция w=arg(z) является непрерывной
нам всей комплексной плоскости, за исключением точек z=0, z= , и точек, лежащей на положительной части действительной полуоси.
, и точек, лежащей на положительной части действительной полуоси.
Основное определение.Функция
комплексной переменной f(z), zО
g, называется непрерывной в
области g, если она непрерывна в "
zО g.
Обозначение: f(z)О
C(g).
Аналогично определяются понятия f(z)О
C(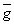 ),
и f(z)О C(
),
и f(z)О C( ).
При этом при определении непрерывности по Гейне в zО
).
При этом при определении непрерывности по Гейне в zО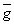 или
zО
или
zО надо рассматривать последовательности {zn},
состоящие только из точек znО
надо рассматривать последовательности {zn},
состоящие только из точек znО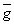 или
znО
или
znО .
.
Замечание 4. В случае понятия
непрерывности по Коши для f(z)О
C(g) для заданного e d
зависит от (e ,z) (d
=d (e
,z)), т.е. на e
- окрестность "
точки w=f(z)О
D отображается d
-окрестность соответствующей точки z, где d
для различных z- различна.