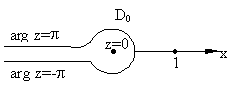
f(z)
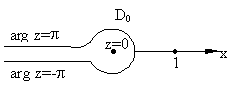 |
f(z)= f(z) |
Теорема 14.2
Пусть функции wi=fi(z)![]() C
C![]() (gi)
и [ai,bi]
(gi)
и [ai,bi]![]() gi,
wi
gi,
wi![]() Di.
И пусть F (z)=F[w1,..., wn]
является аналитической функцией каждой из переменных wi
Di.
И пусть F (z)=F[w1,..., wn]
является аналитической функцией каждой из переменных wi![]() Di.
Тогда из соотношения F[f1(x1),...,fn(xn)]=0,
xi
Di.
Тогда из соотношения F[f1(x1),...,fn(xn)]=0,
xi![]() [ai,bi]
(*) =>F[f1(z1),...,fn(zn)]=0,
zi
[ai,bi]
(*) =>F[f1(z1),...,fn(zn)]=0,
zi![]() gi.
gi.
Доказательство. Докажем
для случая n=2. В общем случае доказательство аналогичное. Фиксируем x°2![]() [a2,b2]
и рассмотрим
F 1(z1)=F[f1(z1),f2(x°2)]
[a2,b2]
и рассмотрим
F 1(z1)=F[f1(z1),f2(x°2)]![]() C
C![]() (g1).
По теореме 14.1 *)
из (*) => F 1(z1)
(g1).
По теореме 14.1 *)
из (*) => F 1(z1)![]() 0,
z1
0,
z1![]() g1.
Т.к. x°2-
произвольное, то => F[f1(z1),f2(x2)]=0,
z1
g1.
Т.к. x°2-
произвольное, то => F[f1(z1),f2(x2)]=0,
z1![]() g1,
g1,
x2![]() [a2,b2]
(**) . Фиксируем z°1
[a2,b2]
(**) . Фиксируем z°1![]() g1
и рассмотрим F 2(z2)=F[f1(z°1),f2(z2)]
g1
и рассмотрим F 2(z2)=F[f1(z°1),f2(z2)]![]() C
C![]() (g2).
(g2).
Из (**) =>F2(z2)![]() 0,
z2
0,
z2![]() g2 => F[f1(z°1),f2(z2)]=0,
z2
g2 => F[f1(z°1),f2(z2)]=0,
z2![]() g2 . Т.к.
z°1-
любое из g1 то F[f1(z1),f2(z2)]=0,
z1
g2 . Т.к.
z°1-
любое из g1 то F[f1(z1),f2(z2)]=0,
z1![]() g1, z2
g1, z2![]() g2.
n
g2.
n
Примеры.
1. sin(z1+z2)=sinz1cosz2+cosz1sinz2"
z1,z2 и другие тригонометрические
формулы для функций разных аргументов.
2. w=f(z)=ez-
аналитическое продолжение ex
на всю комплексную плоскость. Т.к. ex1+x2= ex1
ex2=> ez1+z2= ez1 ez2,
в частности ez=ex+iy=ex eiy=w
=> =>|w|=ex, arg w=y - показательная
функция w= ez производит
отображение прямой y=y0
на плоскости z на луч arg w=y0
на плоскости w. Полоса g0(-p
<Imz<p )![]() D0(-p
<arg w<p
)- плоскость с разрезом по отрицательной части вещественной оси,
причем граничной прямой Imz=-p
соответствует нижний берег разреза, а прямой Imz=p
- верхний берег разреза.
D0(-p
<arg w<p
)- плоскость с разрезом по отрицательной части вещественной оси,
причем граничной прямой Imz=-p
соответствует нижний берег разреза, а прямой Imz=p
- верхний берег разреза.
Обратная функция z=ln0 w=x+i y=ln |w|+i arg w.
Аналогично, g1(p
<Imz<3p )![]() D1(p
<arg w<3p
). Чтобы при непрерывном переходе точки z из g0 в
g1 через Imz=p
образ этой точки непрерывно переходил из D0
в D1 надо склеить берега
разрезов, соответствующие общему значению arg w=p
. Получим новое геометрическое многообразие - двулистную Риманову
поверхность, состоящую из листов D0
и D1.
D1(p
<arg w<3p
). Чтобы при непрерывном переходе точки z из g0 в
g1 через Imz=p
образ этой точки непрерывно переходил из D0
в D1 надо склеить берега
разрезов, соответствующие общему значению arg w=p
. Получим новое геометрическое многообразие - двулистную Риманову
поверхность, состоящую из листов D0
и D1.
Аналогично gn((2n-1)p
<Imz<(2n+1)p )![]() Dn((2n-1)p
<arg w<(2n+1)p
). Полная комплексная плоскость Z
Dn((2n-1)p
<arg w<(2n+1)p
). Полная комплексная плоскость Z ![]() бесконечнолистную
Риманову поверхность, склеенную из листов Dn,
причем лист Dn склеен с
листами Dn+1 и Dn-1
по берегам разрезов на которых arg w принимает одинаковые значения. На
этой Римановой поверхности определена обратная функция z=Ln w =ln|w|+iArg
w, -
бесконечнолистную
Риманову поверхность, склеенную из листов Dn,
причем лист Dn склеен с
листами Dn+1 и Dn-1
по берегам разрезов на которых arg w принимает одинаковые значения. На
этой Римановой поверхности определена обратная функция z=Ln w =ln|w|+iArg
w, -![]() <
Arg w<
<
Arg w<![]() .
.
На обычной комплексной плоскости w функция
z=Ln w является бесконечнозначной (многозначной). На каждом
листе- определенная ветвь lnn w. w=ez=eLnw.
Функция w=ez - периодическая
с мнимым периодом 2pi : ez=
ez+2pi . ez- бескончнолистная
(многолистная).
Особая роль
точки w=0.
При обходе точки w0![]() 0
по достаточно малому замкнутому контуру, мы все время остаемся на одном
и том же листе Dn, или возвращаемся
на этот лист, дважды пересекая разрез, заходя на Dn-1(Dn+1).
При этом, после обхода значение lnn w
не изменится.
0
по достаточно малому замкнутому контуру, мы все время остаемся на одном
и том же листе Dn, или возвращаемся
на этот лист, дважды пересекая разрез, заходя на Dn-1(Dn+1).
При этом, после обхода значение lnn w
не изменится.
При обходе точки w=0 мы пересечем разрез
только один раз и с одной ветви lnn w
(lnn w0 = ln |w0|+i arg w0,
(2n-1)p <arg w0<(2n+1)p
) перейдем надругую ветвь
lnn-1 w (lnn-1
w0
= ln |w0|+i arg w0, (2n-3)p
<arg w0<(2n-1)p
).
Точка w=0 - точка
ветвления функции z=Ln w. Причем для Ln w точка w=0- точка ветвления
бесконечного порядка.
Аналогичными свойствами обладает бесконечно
удаленная точка w=w![]() .Определение.
Если для точки z0 можно указать
такую e
-окрестность, что при однократном обходе точки z0
по " замкнутому
контуру
.Определение.
Если для точки z0 можно указать
такую e
-окрестность, что при однократном обходе точки z0
по " замкнутому
контуру ![]() этой e
-окрестности, происходит переход с одной ветви многозначной функции на
другую, то точка z0 называется
точкой
ветвления (разветвления) данной многозначной функции.
этой e
-окрестности, происходит переход с одной ветви многозначной функции на
другую, то точка z0 называется
точкой
ветвления (разветвления) данной многозначной функции.
В окрестности точки ветвления отдельные
ветви многозначной функции уже нельзя рассматривать как отдельные однозначные
функции, поскольку при обходе точки ветвления их значения меняются.
1. Для функций w=f1(z)=![]() и
w=f2(z)=
и
w=f2(z)=![]() точки z=0 и точки z=╠
1 соответственно являются точками ветвления второго порядка (Разобрать
самостоятельно!).
точки z=0 и точки z=╠
1 соответственно являются точками ветвления второго порядка (Разобрать
самостоятельно!).
2. f(z)=za
, где a - "
число, действительное или комплексное.
f(z)=ea Lnz= ea(ln|z|+iArg
z).
При a
=n: ein(arg z+2p k)= ein arg
z => f(z)- однозначная (но многолистная,
n-листная.).
При a
=n/m - f(z) принимает m различных значений (многозначная).
При a
иррациональном или комплексном f(z) принимает бесконечное число значений
(многозначная).
1i=eiLn1= ei(ln|1|+i2p k)= e-2p k, k=0, ╠1, ╠2 ... .
Тригонометрические функции являются бесконечнолистными периодическими функциями.