Пусть f(z)
j(z)=
dx = ir eijdj , получим
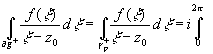 f(x
)dj =i
f(x
)dj =iОценим I. | I |
|f(x )-f(z0)|< e, как только |x (r )-z0|<d. А это значит, что при r
 .
.
Замечания.
1. Формула верна как для g односвязной, так и g- многосвязной, только в последнем случае
![]() 7.
Интегральная
формула Коши. (Интеграл Коши)
7.
Интегральная
формула Коши. (Интеграл Коши)
Пусть f(z)![]() C
C![]() (
(![]() ).
Выразим f(z0) z0
).
Выразим f(z0) z0 ![]() g через значения f(z) на
g через значения f(z) на ![]() .
Рассмотрим
.
Рассмотрим
j(z)=![]()
![]() C
C![]() (
(![]() /z0).
Поэтому, если в области g взять такой замкнутый контур g
, чтобы точка z0 попала
внутрь ограниченной им области, то j
(z) будет аналитической в двухсвязной области g*,
заключенной между
/z0).
Поэтому, если в области g взять такой замкнутый контур g
, чтобы точка z0 попала
внутрь ограниченной им области, то j
(z) будет аналитической в двухсвязной области g*,
заключенной между ![]() и g . По
теореме Коши для многосвязной области *)
интеграл от функции j(z)
по кривой
и g . По
теореме Коши для многосвязной области *)
интеграл от функции j(z)
по кривой ![]() +g
равен 0:
+g
равен 0: ![]() .
Т.к.
.
Т.к. ![]() ,
то
,
то ![]() .
Поскольку
интеграл, стоящий слева не зависит от выбора контура, то эти свойством
обладает и интеграл, стоящий справа. Удобно в качестве контура интегрирования
выбрать окружность gr
с центром в точке z0 и радиуса
r
. Положив на g r
x
= z0+r eij,
.
Поскольку
интеграл, стоящий слева не зависит от выбора контура, то эти свойством
обладает и интеграл, стоящий справа. Удобно в качестве контура интегрирования
выбрать окружность gr
с центром в точке z0 и радиуса
r
. Положив на g r
x
= z0+r eij,
dx = ir eijdj
, получим 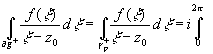 f(x
)dj =i
f(x
)dj =i![]() [f(x
)-f(z0)]dj + i
[f(x
)-f(z0)]dj + i![]() f(z0)dj
=I+2p f(z0).
f(z0)dj
=I+2p f(z0).
Оценим I. | I |![]() 2p
2p![]() |f(x
)-f(z0)|. Устремим r
|f(x
)-f(z0)|. Устремим r![]() 0 при этом. x (r
)
0 при этом. x (r
)![]() z0.Т.к.
f(z)- аналитическая, а следовательно непрерывная в g, то для "e
>0 $ d (e
)>0 такое, что
z0.Т.к.
f(z)- аналитическая, а следовательно непрерывная в g, то для "e
>0 $ d (e
)>0 такое, что
|f(x )-f(z0)|< e,
как только |x (r
)-z0|<d.
А это значит, что при r![]() 0 I
0 I![]() 0.
Поскольку левая часть и второе слагаемое правой части не зависят от r
, то переходя к пределу в обоих частях, получиминтегральную
формулу Коши: f(z0)=
0.
Поскольку левая часть и второе слагаемое правой части не зависят от r
, то переходя к пределу в обоих частях, получиминтегральную
формулу Коши: f(z0)= .
.
Замечания.
1. Формула верна как для g односвязной, так и g-
многосвязной, только в последнем случае ![]() +-
полная граница области, проходимая в положительном направлении.
+-
полная граница области, проходимая в положительном направлении.
2. Интеграл
вида I(z0)= имеет смысл для "
положения точки z0 на комплексной
плоскости при условии, что z0
имеет смысл для "
положения точки z0 на комплексной
плоскости при условии, что z0 |
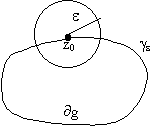 |
 ,
где ge
представляет собой часть контура
,
где ge
представляет собой часть контура 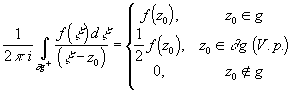
Следствия интегральной формулы Коши.
Пусть f(z)О
C![]() (g ).
(g ).
1 Формула
среднего значения. Пусть z0-
некоторая внутренняя точка односвязной области g. Возьмем окружность с
центром в
z0
и радиусом
R, целиком лежащую в g. Тогда f (z0)=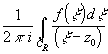 =
(x = z0+R eij)=
=
(x = z0+R eij)=![]()
![]() f(z0+Reij)dj
=
f(z0+Reij)dj
=![]()
![]() f(x )ds ,
f(x )ds ,
(ds=Rdj, круг
KR![]() g)-
формула
среднего значения.
g)-
формула
среднего значения.
2. Принцип максимума модуля.Если
f(z)![]() C
C![]() (
(![]() )
и f(z)
)
и f(z)![]() const, то |f(z)|
достигает своего максимального значения только на
const, то |f(z)|
достигает своего максимального значения только на ![]() .
.
Доказательство (от противного). Пусть
$
z0![]() g: |f(z0)|=M
g: |f(z0)|=M ![]() |f(z)|, для " z
|f(z)|, для " z![]()
![]()
. M=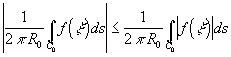
![]() M =>
M => ![]() =M.
=M.
(C0-окружность |z-z0|=R0,
C0![]() g;
x
= z0+R0eij,
ds=R0dj )=>|f(x
)|=M (для " x
g;
x
= z0+R0eij,
ds=R0dj )=>|f(x
)|=M (для " x![]() C0). Действительно, |f(x
)|
C0). Действительно, |f(x
)| ![]() M для " x
M для " x![]() C0 по предположению. Далее, пусть
в некоторой точке x0
C0 по предположению. Далее, пусть
в некоторой точке x0![]() C0 выполнено |f(x0)|<M.
Тогда, т.к. |f(x )| непрерывен на C0
, то $ дуга g0
C0 выполнено |f(x0)|<M.
Тогда, т.к. |f(x )| непрерывен на C0
, то $ дуга g0
длины L0 -некоторая окрестность
точки x0 (x0![]() g0),
на которой |f(x )|
g0),
на которой |f(x )|![]() M-e , e
>0 (а на остальной части окружности |f(x
)| =M для " x
M-e , e
>0 (а на остальной части окружности |f(x
)| =M для " x![]() C0/g0).
Тогда
C0/g0).
Тогда
![]()
![]()
![]() (M-e
)L0/2pR0+M(2pR0-L0)/2pR0=M-e
L0/2pR0<M
=> M<M. Чего быть не может. => |f(x
)|=M (для "x
(M-e
)L0/2pR0+M(2pR0-L0)/2pR0=M-e
L0/2pR0<M
=> M<M. Чего быть не может. => |f(x
)|=M (для "x![]() C0)
=> |f(x )|=M (x
C0)
=> |f(x )|=M (x![]() C':
|z-z0|=R'<R0) => |f(x
)|=M (x
C':
|z-z0|=R'<R0) => |f(x
)|=M (x![]() K0
:
|z-z0|
K0
:
|z-z0|![]() R0) => |f(z*)|=M для
"
z*
R0) => |f(z*)|=M для
"
z*![]() g.
g.
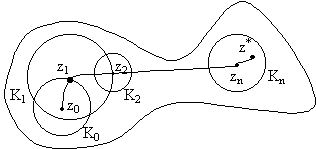 |
Покажем это. Соединим
точки z0
и z*
кривой L |z-z1| |
Замечания.
1. Если f(z)![]() C
C![]() (
(![]() )
и f(z)
)
и f(z)![]() 0 для
"
z
0 для
"
z![]()
![]() ,
то имеет место принцип минимума модуля. Для доказательства
достаточно рассмотреть функцию j
(z)=1/f(z) и воспользоваться принципом максимума модуля *).
,
то имеет место принцип минимума модуля. Для доказательства
достаточно рассмотреть функцию j
(z)=1/f(z) и воспользоваться принципом максимума модуля *).
2. Теорема верна как
для односвязной, так и для многосвязной области.
3. Геометрическая
интерпретация.
Действительные функции двух действительных
переменных u(x,y) и v(x,y)- вещественная и мнимая части аналитической
функции f(z) не имеют в g локальных
экстремумов, а могут иметь лишь седловые точки. Линии равного уровня этих
функций (если f![]() const)
не замкнуты, т.е. упираются в границу области g, либо уходят на бесконечность
в случае неограниченной области. Внутри области g нет точек, в которых
эти функции возрастают или убывают по всем направлениям.
const)
не замкнуты, т.е. упираются в границу области g, либо уходят на бесконечность
в случае неограниченной области. Внутри области g нет точек, в которых
эти функции возрастают или убывают по всем направлениям.
Важное обобщение.
![]() 8.
Интеграл
типа Коши.
8.
Интеграл
типа Коши.
Пусть C- кусочно-гладкая
кривая конечной длины L: ![]() ds=L
и f(x ) непрерывна в"
точкеx
ds=L
и f(x ) непрерывна в"
точкеx![]() C. Тогда при z
C. Тогда при z![]() C $ F(z)=
C $ F(z)=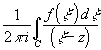 - интеграл
типа Коши.
- интеграл
типа Коши.
Теорема 8.1. В "
z0![]() C
F(z0)- дифференцируема и
F'(z0)=
C
F(z0)- дифференцируема и
F'(z0)=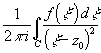 .
.
Доказательство. Пусть
z0 и z0+D
z ![]() C. Т.к. z0
C. Т.к. z0![]() C,
то $d 0>0
и d0>0 такие, что :замкнутый
круг |z-z0|
C,
то $d 0>0
и d0>0 такие, что :замкнутый
круг |z-z0|![]() d0
,будет
находиться на конечном расстоянии d0>0
от кривой C. Пусть |D z|<d0.
Тогда для "x
d0
,будет
находиться на конечном расстоянии d0>0
от кривой C. Пусть |D z|<d0.
Тогда для "x![]() С: |x -z0|>d0,
|x -z0-D
z |>d0.
С: |x -z0|>d0,
|x -z0-D
z |>d0.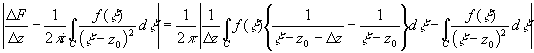 =
=
=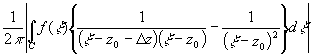 =
=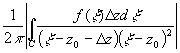
![]()
![]()
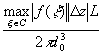 <e
при |D z|<d
<d 0=> $
<e
при |D z|<d
<d 0=> $![]() =F'(z0)=
=F'(z0)=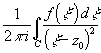 n.
n.
Замечание.
Непрерывность F'(z), z![]() C доказывается аналогично с помощью оценки |D
F'(z)|.
C доказывается аналогично с помощью оценки |D
F'(z)|.
Теорема 8.2.
При z![]() C
F(z)
C
F(z)![]() C
C![]() (E\C).
Уже доказана.
(E\C).
Уже доказана.
Теорема
8.3. При zП
C F(z) имеет непрерывные n-е производные для "
n, причем F(n)(z)= .
Доказывается методом математической индукции.
.
Доказывается методом математической индукции.
Теорема 8.4.
(Основная!). Если f(z)![]() C
C![]() (g),
то для
"
n и " z
(g),
то для
"
n и " z![]() g
$ f(n)(z)
g
$ f(n)(z)![]() C
C![]() (g).
(g).
Доказательство. Пусть z0![]() g.
Построим замкнутый контур C, содержащий z0,
который можно стянуть к z0,
оставаясь все время в g. Тогда в силу интегральной формулы Коши *)
f(z0)=
g.
Построим замкнутый контур C, содержащий z0,
который можно стянуть к z0,
оставаясь все время в g. Тогда в силу интегральной формулы Коши *)
f(z0)=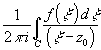 ,
но это интеграл типа Коши => $ f(n)(z0)=
,
но это интеграл типа Коши => $ f(n)(z0)=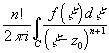 => f(n)(z0)
=> f(n)(z0)![]() C
C![]() (g)
для " z0
(g)
для " z0![]() g
n.
g
n.
Итак, если функция f(z) является аналитической
в g, то у нее в g $
непрерывные производные всех порядков. Это существенное отличие от функции
действительной переменной имеющей непрерывную первую производную в некоторой
области, для которой из существования первой производной, вообще говоря,
не следует существование высших производных. Например, функция y(x)=x|x|
непрерывна на всей числовой прямой; ее производная y'(x)=2|x|
также непрерывна на всей числовой прямой,
однако, y"(0) не существует .
Дальнейшие следствия теоремы Коши *) и интеграла Коши *).
Теорема Морера.
Если f(z)![]() C(g), g-односвязная и для " g
C(g), g-односвязная и для " g![]() g:
g: ![]() f(z)dz=0,
где g -замкнутый
контур, который можно стянуть в точку, оставаясь в g, то f(z)
f(z)dz=0,
где g -замкнутый
контур, который можно стянуть в точку, оставаясь в g, то f(z)![]() C
C![]() (g).
(g).
Доказательство. При условиях
теоремы $ F(z)=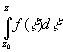
![]() C
C![]() (g) (Теорема 6.1*),
где z0 и z- произвольные
точки g, а интеграл берется по "
пути
(g) (Теорема 6.1*),
где z0 и z- произвольные
точки g, а интеграл берется по "
пути![]() g, соединяющему эти точки. При
этом F'(z)=f(z). Но производная аналитической функции сама является аналитической
функцией (теорема 8.4 *),
т.е. $ F"(z)
g, соединяющему эти точки. При
этом F'(z)=f(z). Но производная аналитической функции сама является аналитической
функцией (теорема 8.4 *),
т.е. $ F"(z)![]() C(g) а именно F"(z)=f'(z)
C(g) а именно F"(z)=f'(z)![]() C(g).n
C(g).n
Замечание.
1. Теорема Морера является
в некотором смысле обратной к теореме Коши *).
2. Теорема 8.4 *)
и Теорема Морера справедливы и для многосвязных ообластей.
Теорема Лиувилля.
Если f(z)![]() C
C![]() (E) и f(z)
(E) и f(z)![]() const,
то при z
const,
то при z![]()
![]() , |f(z)|
, |f(z)|![]()
![]() .
.
Другая формулировка:
Если f(z)![]() C
C![]() (E) и $ M: |f(z)|
(E) и $ M: |f(z)|![]() M для " z (|f(z)|-
равномерно ограничен), то f(z)
M для " z (|f(z)|-
равномерно ограничен), то f(z)![]() const.
const.
Доказательство. f'(z)=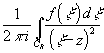 .,
где CR: |x
-z|=R. По условию теоремы $ M:
.,
где CR: |x
-z|=R. По условию теоремы $ M:
|f(z)|![]() M, независимо
от R => |f'(z)|
M, независимо
от R => |f'(z)|![]() 2p RM/2p R2=M/R.
Т.к. R можно выбрать сколь угодно большим (R
2p RM/2p R2=M/R.
Т.к. R можно выбрать сколь угодно большим (R![]()
![]() ), а f'(z) не зависит от R, то |f'(z)|=0. В силу произвольности выбора
z, |f'(z)|=0 на всей комплексной плоскости E=>f(z)
), а f'(z) не зависит от R, то |f'(z)|=0. В силу произвольности выбора
z, |f'(z)|=0 на всей комплексной плоскости E=>f(z)![]() const
для " z.n
const
для " z.n
Определение.
f(z)![]() C
C![]() (E)(на всей комплексной плоскости) (z
(E)(на всей комплексной плоскости) (z![]()
![]() ) называется
целой функцией.
) называется
целой функцией.
Целая функция![]() const не может быть ограничена по абсолютной величине.
const не может быть ограничена по абсолютной величине.
Так например, целые функции sin z и cos
z неограничены по модулю!
Пример целой функции. Функция
f(z)=zn.
Отображение области однолистности*)
Сектор раскрыва 2p
/n отображается на всю комплексную плоскость.
Важное замечание. Конфомное
отображение плоскости с выколотой точкой или расширенной плоскости на единичный
круг невозможно!