Лекция 10.
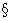 18.
Вычисление несобственных интегралов I-го рода от функции действительной
переменной с помощью вычетов.
18.
Вычисление несобственных интегралов I-го рода от функции действительной
переменной с помощью вычетов.
Лемма
18.1 Пусть f(z) C
C (|z|>R0
(|z|>R0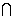 Imz>0),
за исключением конечного числа изолированных особых точек и |f(z)|<M/|z|1+d,
d
>0. Тогда
Imz>0),
за исключением конечного числа изолированных особых точек и |f(z)|<M/|z|1+d,
d
>0. Тогда 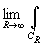 f(x
)dx =0.
f(x
)dx =0.
(C'R- полуокружность |z|=R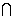 Imz>0).
Imz>0).
Доказательство.
При R>R0: |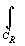 f(x
)dx |
f(x
)dx |
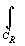 |f(x
)|ds<Mp R/R1+d=
Mp /Rd
|f(x
)|ds<Mp R/R1+d=
Mp /Rd 0
при R
0
при R
 n
.
n
.
Замечания.
1. Если условия Леммы 18.1 выполнены при j1<arg
z<j 2,
то 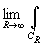 f(x
)dx =0.
f(x
)dx =0.
(C'R- дуга окружности, лежащая
в данном секторе: |z|=R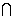 (j1<arg
z<j2))
(j1<arg
z<j2))
2. Условия Леммы 18.1
будут выполнены, если f(z) является аналитической в окрестности z ,
которая является нулем не ниже второго порядка для f(z).
,
которая является нулем не ниже второго порядка для f(z).
Теорема 18.1.
Пусть f(x) задана при - <x<
<x< и $ аналитическое
продолжение f(z) на Im z
и $ аналитическое
продолжение f(z) на Im z 0, имеющее
конечное число изолированных особых точек zn,
не имеющее особых точек на действительной оси и удовлетворяющее условиям
Леммы 18.1 *)
. Тогда $
несобственный интеграл I-го рода
0, имеющее
конечное число изолированных особых точек zn,
не имеющее особых точек на действительной оси и удовлетворяющее условиям
Леммы 18.1 *)
. Тогда $
несобственный интеграл I-го рода 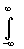 f(x)dx=2p
i
f(x)dx=2p
i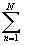 Выч[f(z),zn].
Выч[f(z),zn].
Доказательство. При R>R0
рассмотрим замкнутый контур(-R<x<R) C'R{|z|=R
C'R{|z|=R Imz>0}.
По основной теореме теории вычетов *)
Imz>0}.
По основной теореме теории вычетов *)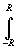 f(x)dx+
f(x)dx+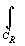 f(x
)dx =2p i
f(x
)dx =2p i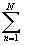 Выч[f(z),zn].
Но, по Лемме 18.1 *)
Выч[f(z),zn].
Но, по Лемме 18.1 *)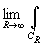 f(x
)dx =0, правая
часть не зависит от R =>
f(x
)dx =0, правая
часть не зависит от R =>
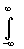 f(x)dx=2p
i
f(x)dx=2p
i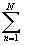 Выч[f(z),zn]
n
.
Выч[f(z),zn]
n
.
Замечания.
1. Если f(x)- четная (f(-x)=f(x)) и удовлетворяет
условиям Теоремы 18.1, то
 f(x)dx=p
i
f(x)dx=p
i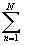 Выч[f(z),zn]
Выч[f(z),zn]
2. Имеет место аналогичная
теорема, когда аналитическое продолжение f(x) в нижнюю полуплоскость удовлетворяет
условиям, аналогичным условиям Леммы 18.1 *)
для нижней полуплоскости.
Пример.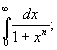 f(z)=
f(z)=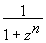 ; ; 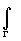 f(z)dz= f(z)dz=
=2p iВыч[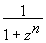 ,eip
/n]=(z0=eip /n-полюс
1-порядка)= ,eip
/n]=(z0=eip /n-полюс
1-порядка)=
=2p
i/(neip (n-1)/n)=-2p
i/(ne-ip /n).
С другой стороны, |
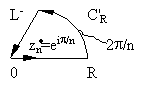 |
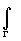 f(z)dz=
f(z)dz=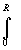 f(z)dz+
f(z)dz+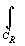 f(x
)dx +
f(x
)dx +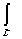 f(z)dz
.При R
f(z)dz
.При R
 второе слагаемое
второе слагаемое  0
0
(по Замечанию 1 к Лемме 18.1 *)
. В третьем слагаемом z=xei2p /n
(f(xei2p
/n)=f(x)). Устремив R
 , получим
, получим  f(x)dx-ei2p
/n
f(x)dx-ei2p
/n f(x)dx=
(1-ei2p /n)
f(x)dx=
(1-ei2p /n) f(x)dx=-2p
i/(ne-ip /n) =>
f(x)dx=-2p
i/(ne-ip /n) => f(x)dx=-2p
i/[(ne-ip /n) (1-ei2p
/n)]= p /(n sin p
/n).
f(x)dx=-2p
i/[(ne-ip /n) (1-ei2p
/n)]= p /(n sin p
/n).
Лемма
18.2 (Жордана). Если f(z) C
C (|z|>R0
(|z|>R0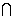 Imz>0)
за исключением конечного числа изолированных особых точек и f(z)=>0 при
|z|
Imz>0)
за исключением конечного числа изолированных особых точек и f(z)=>0 при
|z|
 (равномерно по arg z,
(равномерно по arg z,
0 arg
z
arg
z p ),
z
p ),
z Imz>0,
то при a>0
Imz>0,
то при a>0 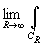 eiaxf(x
)dx =0, C'R-
полуокружность
eiaxf(x
)dx =0, C'R-
полуокружность
|z|=R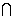 Imz>0.
Imz>0.
Доказательство. "e>
0 $ R : |f(z)|<e(R)
, |z|>R, причем e(R) 0
при R
0
при R
 .
.
При R>R0: |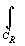 eiaxf(x
)dx |
eiaxf(x
)dx |
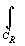 |eiaxf(x
)|ds
|eiaxf(x
)|ds
{x =Reij=x+iy,x=Rcosj
, y=Rsinj , ds=Rdj
, eiax=eia(x+iy)=
eiaxe-ay, |eiax|=e-ay=e-ay=
=e-aRsinj} e
R e
R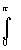 |eiax|dj
=e R |eiax|dj
=e R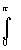 e-aRsinj dj
=2e R
e-aRsinj dj
=2e R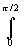 e-aRsinjdj< e-aRsinjdj< |
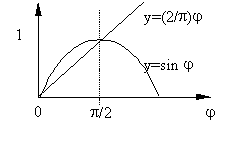 |
<{sinj (2/p
)j при 0
(2/p
)j при 0 j
j p
/2}<2e R
p
/2}<2e R e-aR(2/p
)j dj =pe
(1-e-aR)/a
e-aR(2/p
)j dj =pe
(1-e-aR)/a 0
при R
0
при R
 ,
,
т.к. e(R) 0
при R
0
при R
 (a>0) n .
(a>0) n .
Замечания.
1 Если f(z) удовлетворяет условиям Леммы Жордана
*)
при Imz 0,
0,
то при a<0  eiaxf(x
)dx =0, C'R-
полуокружность |z|=R
eiaxf(x
)dx =0, C'R-
полуокружность |z|=R Imz<0.
Imz<0.
2. Если f(z) удовлетворяет
условиям Леммы Жордана *)
при Rez 0,
0,
то при a=ia
(a >0) 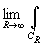 e-axf(x
)dx =0, C'R-
полуокружность |z|=R
e-axf(x
)dx =0, C'R-
полуокружность |z|=R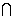 Rez>0.
Rez>0.
3. Если f(z) удовлетворяет
условиям Леммы Жордана *)
при Rez 0,
0,
то при a=-ia
(a >0) 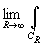 eaxf(x
)dx =0, C'R-
полуокружность |z|=R
eaxf(x
)dx =0, C'R-
полуокружность |z|=R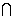 Rez<0.
Rez<0.
4. Лемма Жордана *)
остается справедливой, когда f(z) удовлетворяет условиям Леммы Жордана
*)
при Imz y0 (Rez
y0 (Rez x0;
Imz
x0;
Imz y0; Rez
y0; Rez x0),
y0
(x0)- фиксированное
число, которое может быть как >0, так и <0, а интегрирование производится
по дуге полуокружности |z-i y0|=R
x0),
y0
(x0)- фиксированное
число, которое может быть как >0, так и <0, а интегрирование производится
по дуге полуокружности |z-i y0|=R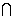 Imz>0
(|z-x0|=R
Imz>0
(|z-x0|=R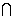 Imz>0; |z-i y0|=R
Imz>0; |z-i y0|=R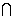 Imz<0;
|z-x0|=R
Imz<0;
|z-x0|=R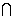 Imz<0).
Доказательство аналогично, но при оценке интеграла следует сделать замену
x
=Reij+iy0
(x
=Reij+x0).
Imz<0).
Доказательство аналогично, но при оценке интеграла следует сделать замену
x
=Reij+iy0
(x
=Reij+x0).
5. Лемма Жордана *)
остается справедливой и при ослабленных условиях на f(z). Пусть f(z) при
Imz>y0 при |z|>R0,
равномерно относительно arg(z-iy1)
при |z|
 f(z)=>0 в секторах -j 0
f(z)=>0 в секторах -j 0 arg(z-iy1)
arg(z-iy1) j1,
p-j2
j1,
p-j2 arg(z-iy1)
arg(z-iy1) p+j0,
и равномерно ограничена в секторе
j 1
p+j0,
и равномерно ограничена в секторе
j 1 arg(z-iy1)
arg(z-iy1) p-j2
, где 0
p-j2
, где 0 j0,j1,j2
j0,j1,j2 p/2
и y1>y0. Тогда
при a>0
p/2
и y1>y0. Тогда
при a>0
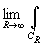 eiaxf(x
)dx =0, C'R-
полуокружность |z-iy1|=R
eiaxf(x
)dx =0, C'R-
полуокружность |z-iy1|=R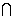 Imz>y0.
Imz>y0.
Теорема 18.2
Пусть f(x) задана при - <x<
<x< и $ аналитическое
продолжение f(z) на Im z
и $ аналитическое
продолжение f(z) на Im z 0, имеющее
конечное число изолированных особых точек zn,
не имеющее особых точек на действительной оси и удовлетворяющее условиям
Леммы Жордана *)
. Тогда $
0, имеющее
конечное число изолированных особых точек zn,
не имеющее особых точек на действительной оси и удовлетворяющее условиям
Леммы Жордана *)
. Тогда $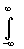 eiaxf(x)dx=2p
i
eiaxf(x)dx=2p
i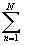 Выч[eiazf(z),zn],
где zn- изолированные особые
точки в верхней полуплоскости Im z
Выч[eiazf(z),zn],
где zn- изолированные особые
точки в верхней полуплоскости Im z 0.
0.
Доказательство. При R>R0
рассмотрим замкнутый контур
(-R<x<R)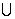 C'R{|z|=R
C'R{|z|=R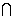 Imz>0}. По основной теореме теории вычетов *)
Imz>0}. По основной теореме теории вычетов *)
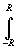 eiaxf(x)dx+
eiaxf(x)dx+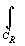 eiaxf(x
)dx =2p i
eiaxf(x
)dx =2p i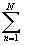 Выч[eiazf(z),zn].
Но, по Лемме Жордана *)
Выч[eiazf(z),zn].
Но, по Лемме Жордана *)
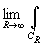 eiaxf(x
)dx =0, правая
часть не зависит от R =>
eiaxf(x
)dx =0, правая
часть не зависит от R =>
=>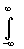 eiaxf(x)dx=2p
i
eiaxf(x)dx=2p
i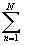 Выч[eiazf(z),zn]
n
.
Выч[eiazf(z),zn]
n
.
Пример. 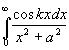 (k>0,
a>0)=
(k>0,
a>0)=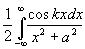 =
= 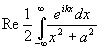 ==
Re p iВыч[
==
Re p iВыч[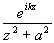 ,ia]
=(z0= ia -полюс 1-порядка)= Re
p
i(e-ka/2ia)=pe-ka/2a.
,ia]
=(z0= ia -полюс 1-порядка)= Re
p
i(e-ka/2ia)=pe-ka/2a.
Замечание. При незначительном
изменении формулировок Лемм 18.1 *)
и 18.2 *)
они остаются справедливыми и в случае бесконечного числа изолированных
особых точек f(z).
Определение.
Функция комплексной переменной f(z) называется мероморфной,
если она определена на всей комплексной плоскости и не имеет в конечной
части плоскости особых точек, отличных от полюсов.
Некоторые интегралы
1. 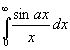 =sign(a)p
/2
=sign(a)p
/2
2. I=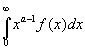 ,
0<a<1; I=
,
0<a<1; I=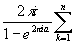 Выч[za-1f(z),zk]
Выч[za-1f(z),zk]
3. I=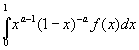 ,
0<a<1; I=
,
0<a<1; I=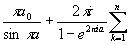 Выч[za-1(1-z)-af(z),zk],
a0=
Выч[za-1(1-z)-af(z),zk],
a0=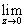 f(z).
f(z).
4. I= f(x)ln(x)dx=p
i
f(x)ln(x)dx=p
i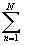 Выч[f(z)(lnz-ip
/2),zk]
Выч[f(z)(lnz-ip
/2),zk]
 19.Логарифмический
вычет.
19.Логарифмический
вычет.
Пусть f(z) C
C (
(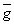 \z1,┘zN),
zn- полюса и f(x
)ч x
\z1,┘zN),
zn- полюса и f(x
)ч x

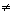 0.
Тогда " x
0.
Тогда " x
 √ правильная и $ f(x
)ч x
√ правильная и $ f(x
)ч x
 .
.
Определение.
Функция j
(z)=f▓(z)/f(z)=[ln f(z)]▓ называется логарифмической производной
функции f(z).
Вычеты j
(z) в ее особых точках zn называются
логарифмическими
вычетами.
Особыми точками j
(z) будут нули z0k и
полюса zk функции f(z).
Как считать вычеты?
a) Пусть z0k
√ нуль порядка n функции f(z); => f(z)=(z-z0k)nf1(z),
f1(z0k)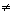 0
=>
0
=>
=> j (z)=n/(z-z0k)+f▓1(z)/f1(z)
=> Выч[j (z),z0k]=n.
b) Пусть zk
√ полюс порядка p функции f(z);=> f(z)=y
(z)/(z-zk)p
, y (zk)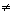 0
=>
0
=>
=> j (z)=-p/(z-zk)+ y
▓(z)/y (z) => Выч[j
(z),zk]=-p.
Теорема 19.1
Если f(z) C
C (
(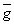 \z1,┘zN),
zn- полюса и f(x
)ч x
\z1,┘zN),
zn- полюса и f(x
)ч x

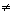 0,
то
0,
то 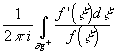 =N-P, где
N- полное число нулей f(z) с учетом кратности, P- полное число полюсов
f(z) с учетом кратности.
=N-P, где
N- полное число нулей f(z) с учетом кратности, P- полное число полюсов
f(z) с учетом кратности.
Доказательство. По основной теореме теории вычетов *)
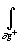 j
(x )dx =2p
i
j
(x )dx =2p
i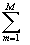 Выч[j
(z),zm]= 2p i[
Выч[j
(z),zm]= 2p i[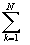 nk-
nk-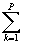 pk]=
2p i(N-P). n
pk]=
2p i(N-P). n
В частности, если f(z) C
C (
(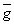 ),
то N=
),
то N=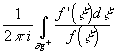 .
.
Принцип аргумента. 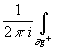 dlnf(x
)=
dlnf(x
)=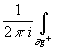 d ln|f(x
)|+
d ln|f(x
)|+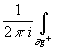 i d arg f(x
). Действительная функция ln|f(x
)| является однозначной функцией, поэтому ее вариация (изменение) при обходе
точкой x
замкнутого контура
i d arg f(x
). Действительная функция ln|f(x
)| является однозначной функцией, поэтому ее вариация (изменение) при обходе
точкой x
замкнутого контура  +
равна 0. => Первое слагаемое =0. Второе слагаемое представляет собой полную
вариацию arg(f(x
)) при обходе точкой x
замкнутого контура
+
равна 0. => Первое слагаемое =0. Второе слагаемое представляет собой полную
вариацию arg(f(x
)) при обходе точкой x
замкнутого контура +,
деленную на 2p
. Итак, N-P=(1/2p )Var[arg(f(x
))]|
+,
деленную на 2p
. Итак, N-P=(1/2p )Var[arg(f(x
))]| + .
+ .
Геометрическая интерпретация.
Изобразим значения w=f(z) точками на комплексной плоскости w. Т.к. f(z) C(
C( ),
то при полном обходе точкой z контура
),
то при полном обходе точкой z контура  на комплексной плоскости z, соответствующая ей точка на плоскости w описывает
некий замкнутый контур С. При этом точка w=0 может оказаться как вне, так
и внутри области, ограниченной контуром C. В первом случае Var[arg(w)]|С=0.
Во втором случае Var[arg(w)]|С= числу полных обходов вокруг
точки w=0, которое совершает точка w при своем движении по контуру C. При
этом точка w может обходить точку w=0 как в положительном направлении (против
часовой стрелки), так и в отрицательном (по часовой).
на комплексной плоскости z, соответствующая ей точка на плоскости w описывает
некий замкнутый контур С. При этом точка w=0 может оказаться как вне, так
и внутри области, ограниченной контуром C. В первом случае Var[arg(w)]|С=0.
Во втором случае Var[arg(w)]|С= числу полных обходов вокруг
точки w=0, которое совершает точка w при своем движении по контуру C. При
этом точка w может обходить точку w=0 как в положительном направлении (против
часовой стрелки), так и в отрицательном (по часовой).
Принцип аргумента. Разность между полным числом нулей и полюсов
функции f(z) в области g определяется числом оборотов, которое совершает
очка w=f(z) вокруг точки w=0, при положительном обходе точкой z контура  .
.
Теорема
Руше Если f(z), j (z) C
C (
(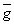 )
и |f(z)|
)
и |f(z)| >|j
(z)|
>|j
(z)|  ,
то N[f+j ]g=N[f]g.
,
то N[f+j ]g=N[f]g.
Доказательство. Для f(z) и F(z)=f(z)+j(z)
выполнены все условия Теоремы 19.1 *)
Действительно, f(z) C
C (
(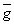 )
=> f(z) |
)
=> f(z) | не имеет особых точек и т.к.
не имеет особых точек и т.к.
|f(z)| >|j
(z)|
>|j
(z)| =>|f(z)|
=>|f(z)|
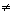 0.
0.
F(z) C
C (
(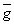 )
=> F(z) |
)
=> F(z) | не имеет особых точек и т.к. |F(z)|
не имеет особых точек и т.к. |F(z)| =|
f(z)+j (z)|
=|
f(z)+j (z)|
 |f(z)|
|f(z)| -
|j (z)|
-
|j (z)| >0. =>N[f+j ]g=(1/2p
)Var[arg(f+j )]
>0. =>N[f+j ]g=(1/2p
)Var[arg(f+j )] ;
N[f]g=(1/2p )Var[arg(f)]
;
N[f]g=(1/2p )Var[arg(f)] ;
;
N[f+j ]g-N[f]g=(1/2p
)Var[arg(f+j )- arg(f)] ={arg
a-arg b=arg a/b т.к. a=|a|eiarga, b=|b|eiargb=>
a/b=(|a|/|b|)ei(arg a-arg b)=> arg a/b = arg a-arg b }=
={arg
a-arg b=arg a/b т.к. a=|a|eiarga, b=|b|eiargb=>
a/b=(|a|/|b|)ei(arg a-arg b)=> arg a/b = arg a-arg b }=
=(1/2p )Var[arg((f+j
)/f)] =(1/2p
)Var[arg(1+j /f)]|
=(1/2p
)Var[arg(1+j /f)]| .
Введем функцию w=1+j
/f. При обходе точкой z контура
.
Введем функцию w=1+j
/f. При обходе точкой z контура  соответствующая ей w опишет некоторую замкнутую кривую C, которая т.к.
|f(z)|
соответствующая ей w опишет некоторую замкнутую кривую C, которая т.к.
|f(z)| >|j
(z)|
>|j
(z)| целиком
будет лежать внутри некоторого круга |w-1|
целиком
будет лежать внутри некоторого круга |w-1| r
<1, т.е. точка w=0 лежит вне кривой С. => Var[arg(1+j/f)]|
r
<1, т.е. точка w=0 лежит вне кривой С. => Var[arg(1+j/f)]| =0
n
.
=0
n
.
Основная
теорема высшей алгебры. Полином n-ой степени имеет на комплексной
плоскости ровно n нулей (с учетом их кратности).
Доказательство. Представим полином F(z)=a0zn+a1zn-1+┘+an
в виде F(z)=f(z)+j
(z), где f(z)=a0zn, j
(z)= a1zn-1+┘+an.
Составим отношение j (z)/f(z)=(a1/a0)1/z+┘+(an/a0)1/zn.
Для "
a0, a1, an $
R0, что для "
|z|=R> R0 0<|j
(z)/f(z)||z|=R<1.
В силу Теоремы Руше *)
N[F] |z|=R= N[f] |z|=R.
Но функция f(z)=a0zn
на всей комплексной плоскости имеет единственный n-кратный нуль- точку
z=0.=> N[F] |z|=R= N[f] |z|=R=n n

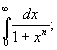 f(z)=
f(z)=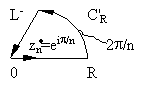
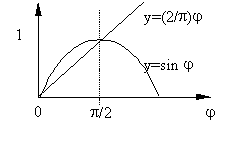
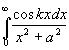 (k>0,
a>0)=
(k>0,
a>0)=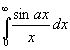 =sign(a)p
/2
=sign(a)p
/2
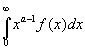 ,
0<a<1; I=
,
0<a<1; I=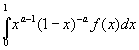 ,
0<a<1; I=
,
0<a<1; I=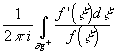 =N-P, где
N- полное число нулей f(z) с учетом кратности, P- полное число полюсов
f(z) с учетом кратности.
=N-P, где
N- полное число нулей f(z) с учетом кратности, P- полное число полюсов
f(z) с учетом кратности.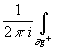 dlnf(x
)=
dlnf(x
)=