Лекция 9.
 15.
Ряд Лорана.
15.
Ряд Лорана.
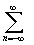 cn(z-z0)n=
cn(z-z0)n=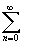 cn(z-z0)n+
cn(z-z0)n+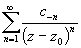 =P(z)+Q(z).
P(z) называется правильной частью ряда Лорана, Q(z)- главной
частью ряда Лорана. P(z)
=P(z)+Q(z).
P(z) называется правильной частью ряда Лорана, Q(z)- главной
частью ряда Лорана. P(z)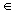 C
C (|z-z0|<R1).
(|z-z0|<R1).
В какой области Q(z) будет аналитической функцией? Сделаем замену
1/(z-z0)=x ;
Q(z) Q(x
)=
Q(x
)= c-nxn
c-nxn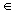 C
C (|x
|<1/R2), где мы обозначили
через
1/R2 радиус сходимости полученного
степенного ряда. При R2<R1
существует
общая область сходимости-
круговое кольцо R2<|z-z0|<R1.
(|x
|<1/R2), где мы обозначили
через
1/R2 радиус сходимости полученного
степенного ряда. При R2<R1
существует
общая область сходимости-
круговое кольцо R2<|z-z0|<R1.
Следствия теоремы Абеля *)
:
1. 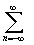 cn(z-z0)n
cn(z-z0)n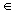 C
C (R2<|z-z0|<R1).
(R2<|z-z0|<R1).
2. Внутри кругового
кольца сходимости ряд Лорана можно почленно дифференцировать и интегрировать
любое число раз, при этом полученные ряды также 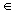 C
C (R2<|z-z0|<R1).
(R2<|z-z0|<R1).
3. R1 определяется
через {cn}, n=0,..., : R1=1/L1, L1=
: R1=1/L1, L1=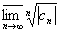 или L1=
или L1=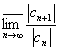 ,
а R2-через {c-n},
n=1,...,
,
а R2-через {c-n},
n=1,..., : R2=
: R2=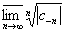 ,
или R2=
,
или R2= .
.
4. Коэффициенты ряда
Лорана cn через значения
суммы ряда в точке z0 не
определяются! В точке z0 сумма
ряда Лорана не определена!
Теорема
15.1 Если f(z)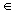 C
C (R2<|z-z0|<R1),
то она однозначно разложима в этом кольце в ряд Лорана f(z)=
(R2<|z-z0|<R1),
то она однозначно разложима в этом кольце в ряд Лорана f(z)=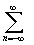 cn(z-z0)n.
cn(z-z0)n.
Доказательство. Фиксируем
произвольную точку z внутри кольца : (R2<|z-z0|<R1)
и построим окружности C'1 : |x
-z0|=R'1 и C'2:
: |x -z0|=R'2,
с центром в точке z0 и радиусами
R'1 и R'2 :
R2<R'2<|z-z0|<R'1<R1.
По формуле Коши для многосвязной области *)
f(z)= +
+ 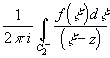 =P(z)+Q(z).
=P(z)+Q(z).
На окружности C'1: |x
-z0|=R▓1 выполняется
неравенство 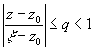 .
Поэтому, дробь 1/(x
-z) можно представить в виде
.
Поэтому, дробь 1/(x
-z) можно представить в виде
1/(x -z)=1/[(x
-z0)-(z-z0)]= и проведя почленное интегрирование, что возможно в силу равномерной сходимости
ряда по переменной x
на CR (см. доказательство
теоремы Тейлора *)
получим P(z)=
и проведя почленное интегрирование, что возможно в силу равномерной сходимости
ряда по переменной x
на CR (см. доказательство
теоремы Тейлора *)
получим P(z)=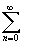 cn(z-z0)n,
где
cn(z-z0)n,
где
cn=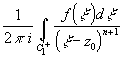 ,
n
,
n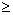 0.
0.
На окружности C'2:
|x -z0|=R▓2 выполняется
неравенство  .
Поэтому, дробь
.
Поэтому, дробь
1/(x
-z) можно представить в виде 1/(x -z)=1/[(x
-z0)-(z-z0)]=
=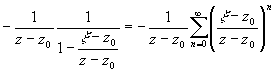 В
результате почленного интегрирования этого ряда получим: Q(z)=
В
результате почленного интегрирования этого ряда получим: Q(z)=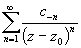 ,
n>0, где c-n=-
,
n>0, где c-n=- .
Изменив направление интегрирования, получим: c-n=
.
Изменив направление интегрирования, получим: c-n=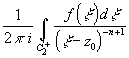 ,
n>0. Подынтегральные функции в выражениях для cn и
c-n являются аналитическими
в круговом кольце R2<|z-z0|<R1.
Поэтому
в силу теоремы Коши *)
значения соответствующих интегралов не изменится при произвольной деформации
контуров интегрирования в области аналитичности подынтегральных функций.
Это позволяет записать общее выражение cn=
,
n>0. Подынтегральные функции в выражениях для cn и
c-n являются аналитическими
в круговом кольце R2<|z-z0|<R1.
Поэтому
в силу теоремы Коши *)
значения соответствующих интегралов не изменится при произвольной деформации
контуров интегрирования в области аналитичности подынтегральных функций.
Это позволяет записать общее выражение cn= ,
n=0,╠ 1, ╠ 2,┘, где
C- произвольный замкнутый контур, лежащий в кольце R2<|z-z0|<R1
и
содержащий точку z0 внутри.
Для f(z) окончательно можно записать: f(z)=
,
n=0,╠ 1, ╠ 2,┘, где
C- произвольный замкнутый контур, лежащий в кольце R2<|z-z0|<R1
и
содержащий точку z0 внутри.
Для f(z) окончательно можно записать: f(z)= cn(z-z0)n+
cn(z-z0)n+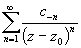 =
=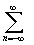 cn(z-z0)n,
где cn=
cn(z-z0)n,
где cn= .
.
Т.к. z-произвольная точка внутри кольца
R2<|z-z0|<R1
=> ряд 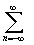 cn(z-z0)n
сходится
к f(z) всюду внутри данного кольца, причем в замкнутом кольце R2<R'2
cn(z-z0)n
сходится
к f(z) всюду внутри данного кольца, причем в замкнутом кольце R2<R'2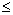 |z-z0|
|z-z0|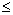 R'1<R1
ряд сходится к f(z) равномерно.
R'1<R1
ряд сходится к f(z) равномерно.
Докажем единственность. Предположим, что
имеет место другое разложение f(z)= 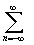 c'n(z-z0)n,
где хотя бы один коэффициент c'n
c'n(z-z0)n,
где хотя бы один коэффициент c'n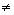 cn.
Тогда всюду внутри кольца R2<|z-z0|<R1
имеет место равенство:
cn.
Тогда всюду внутри кольца R2<|z-z0|<R1
имеет место равенство: 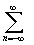 c'n(z-z0)n=
c'n(z-z0)n=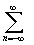 c'n(z-z0)n.
Проведем окружность CR,
радиуса R, R2<R<R1,
с центром в точке z0. Тогда
ряды
c'n(z-z0)n.
Проведем окружность CR,
радиуса R, R2<R<R1,
с центром в точке z0. Тогда
ряды 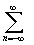 c'n(z-z0)n
и
c'n(z-z0)n
и 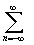 c'n(z-z0)n
сходятся на CR равномерно.
Умножим оба ряда на (z-z0)-m-1,
где m- произвольное целое число и проинтегрируем почленно. Рассмотрим
c'n(z-z0)n
сходятся на CR равномерно.
Умножим оба ряда на (z-z0)-m-1,
где m- произвольное целое число и проинтегрируем почленно. Рассмотрим 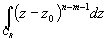 .
Положив z-z0=Reij.,
получим
.
Положив z-z0=Reij.,
получим 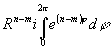 =
=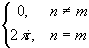 .=>
для произвольного целого m c'm=cm
. n
.=>
для произвольного целого m c'm=cm
. n
Точной областью сходимости ряда Лорана
является круговое кольцо R2<|z-z0|<R1,
на границах которого имеется хотя бы по одной особой точке аналитической
функции f(z), к которой (к функции) сходится данный ряд. (см. Теорему 13.1
*)
 16.
Изолированные особые точки однозначной аналитической функции.
16.
Изолированные особые точки однозначной аналитической функции.
Определение.
Точка z0 называется изолированной
особой точкой функции f(z), если f(z) однозначная и 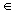 C
C (0<|z-z0|<r
(z0)), а точка z0
является особой точкой *)
функции f(z).
(0<|z-z0|<r
(z0)), а точка z0
является особой точкой *)
функции f(z).
Другими словами, точка z0
называется изолированной особой точкой функции f(z), если
$
такая окрестность точки z0,
в которой нет других особых точек функции f(z).
В самой особой точке z0
функция f(z) может быть не определена. Функцию f(z) в окрестности точки
z0 можно разложить
в ряд Лорана, сходящийся в кольце
0<|z-z0|<r (z0).
Поведение функции f(z) в окрестности точки z0
определяется главной частью ряда Лорана Q(z)=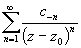 .
.
Важное замечание В
малой
окрестности
точки ветвления и
неизолированной
особой точки вообще нельзя раскладывать в ряд Лорана!
Возможны три
случая:
a) Для "n>0
c-n=0; Q(z)=0; f(z) c0
при z
c0
при z z0- устранимая
особая точка. z0 - правильная
точка f(z). Если функция не определена в точке z0,
то ее можно доопределить по непрерывности, положив f(z0)=c0.
В окрестности устранимой особой точки 0<|z-z0|<r(z0)
: |f(z)|<M и f(z)=(z-z0)mj(z),
m
z0- устранимая
особая точка. z0 - правильная
точка f(z). Если функция не определена в точке z0,
то ее можно доопределить по непрерывности, положив f(z0)=c0.
В окрестности устранимой особой точки 0<|z-z0|<r(z0)
: |f(z)|<M и f(z)=(z-z0)mj(z),
m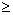 0-
целое, j(z0)
0-
целое, j(z0)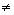 0;
и если
0;
и если 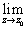 f(z)=0,
то z0- нуль m- того порядка.
f(z)=0,
то z0- нуль m- того порядка.
Теорема 16.1
Если f(z)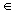 C
C (0<|z-z0|<r(z0))
и |f(z)|<M при 0<|z-с|<r(z0),
то z0- устранимая особая
точка.
(0<|z-z0|<r(z0))
и |f(z)|<M при 0<|z-с|<r(z0),
то z0- устранимая особая
точка.
Доказательство. Разложим f(z) в
ряд Лорана и рассмотрим выражение для коэффициентов главной части. c-n=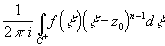 ,
n>0. В качестве контура интегрирования выберем круг с центром в точке z0
и радиуса r: |x
-z0|=r.
Тогда , сделав замену x-z0=reij,
dx =ireijdj
и
учтя, что |einj|=1,
получим оценку: |c-n|<r
Mrn-1
,
n>0. В качестве контура интегрирования выберем круг с центром в точке z0
и радиуса r: |x
-z0|=r.
Тогда , сделав замену x-z0=reij,
dx =ireijdj
и
учтя, что |einj|=1,
получим оценку: |c-n|<r
Mrn-1 0
при r
0
при r 0.
Т.к. значения c-n не зависят
от r , то
c-n=0. n
0.
Т.к. значения c-n не зависят
от r , то
c-n=0. n
b) Ряд Лорана функции
f(z) в окрестности ее изолированной особой точки содержит конечное число
членов с отрицательными степенями; Q(z)=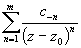 ;
c-m
;
c-m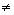 0.
0.
f(z)
 при z
при z z0- полюс
порядка m, f(z)=
z0- полюс
порядка m, f(z)=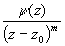 ;
y(z0)
;
y(z0)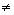 0
0
Теорема 16.2
Если f(z)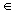 C
C (0<|z-z0|<r(z0)),
z0- изолированная особая точка
f(z) и |f(z)|=>
(0<|z-z0|<r(z0)),
z0- изолированная особая точка
f(z) и |f(z)|=> при z
при z z0
(независимо
от способа стремления z к z0),
то z0- полюс f(z).
z0
(независимо
от способа стремления z к z0),
то z0- полюс f(z).
Доказательство. |f(z)|=> при z
при z z0 =>
для "A>0 $e
: 0<|z-z0|<e,
|f(z)|>A; Рассмотрим g(z)=1/f(z); g(z)
z0 =>
для "A>0 $e
: 0<|z-z0|<e,
|f(z)|>A; Рассмотрим g(z)=1/f(z); g(z)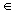 C
C (0<|z-z0|<e
); |g(z)|<1/A=M => z0- устранимая
особая точка g(z) (по Теореме 16.1 *); =>
g(z)=(z-z0)mj(z), m
(0<|z-z0|<e
); |g(z)|<1/A=M => z0- устранимая
особая точка g(z) (по Теореме 16.1 *); =>
g(z)=(z-z0)mj(z), m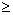 0,
j(z0)
0,
j(z0)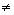 0
=> f(z)=
0
=> f(z)=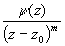 ;
y(z0)
;
y(z0)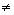 0
n
0
n
c) Точка z0
называется существенно особой
точкой функции f(z), если ряд Лорана функции f(z) в окрестности ее изолированной
особой точки z0 содержит
бесконечно много членов с отрицательными степенями разности (z-z0).
(Бесконечное число коэффициентов c-n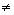 0).
Поведение аналитической функции в окрестности существенно особой точки
описывается следующей теоремой.
0).
Поведение аналитической функции в окрестности существенно особой точки
описывается следующей теоремой.
Теорема
Сохоцкого-Вейерштрасса Для
"
комплексного числа B и "e>0,
в
"h
- окрестности существенно особой точки z0 0<|z-z0|<h
$ z1: |f(z1)-B|<e
.
Доказательство. (От противного)
Пусть $ такие e0
и
h
0: для
"z
0<|z-z0|<h0; |f(z)-B|>e0.
Рассмотрим
g(z)=1/[f(z)-B]=>
|g(z)|=1/|f(z)-B|<1/e0=M. => z0-
устранимая особая точка g(z) (по Теореме 16.1 *);
=> g(z)=(z-z0)mj(z), m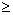 0,
j(z0)
0,
j(z0)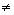 0
=> f(z)=B+
0
=> f(z)=B+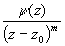 ;
y(z0)
;
y(z0)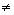 0
=> z0- полюс f(z) m
0
=> z0- полюс f(z) m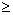 0,
или
правильная точка при m=0. Получили
противоречие. n
0,
или
правильная точка при m=0. Получили
противоречие. n
Замечание 1. {hn} 0
=>{z(n)1}
0
=>{z(n)1} z0.
{f(z(n)1)}
z0.
{f(z(n)1)} B=>
в
окрестности существенно особой точки можно выбрать {z(n)1}
B=>
в
окрестности существенно особой точки можно выбрать {z(n)1} z0
такую, что {f(z(n)1)}
сходится
к " наперед
заданному числу.
z0
такую, что {f(z(n)1)}
сходится
к " наперед
заданному числу.
Пример. f(z)=e1/z
точка z=0 - существенно особая.
Классификация изолированных особых точек
на языке пределов.
Пусть z0- изолированная особая
точка f(z)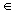 C
C (0<|z-z0|<r
(z0)).
(0<|z-z0|<r
(z0)).
a) Если при z
из
окрестности 0<|z-z0|<r(z0)
и
при z z0
f(z)
z0
f(z) c0 |c0|<
c0 |c0|< ,
то
z0 -устранимая особая
точка f(z).
,
то
z0 -устранимая особая
точка f(z).
b) Если при z
из
окрестности 0<|z-z0|<r
(z0) и при z z0
f(z)
z0
f(z)
 , то z0 -полюс
f(z).
, то z0 -полюс
f(z).
c) Если при z
из
окрестности 0<|z-z0|<r
(z0) и при z z0
f(z) не имеет конечного или бесконечного предела, то z0 -существенно
особая точка f(z).
z0
f(z) не имеет конечного или бесконечного предела, то z0 -существенно
особая точка f(z).
Определение. z является
изолированной особой точкой однозначной аналитической функции, если $R>0
: для
"z
: |z|>R f(z) не имеет особых точек, находящихся
на конечном расстоянии от точки z=0.
является
изолированной особой точкой однозначной аналитической функции, если $R>0
: для
"z
: |z|>R f(z) не имеет особых точек, находящихся
на конечном расстоянии от точки z=0.
Ряд Лорана в окрестности z : f(z)=
: f(z)=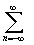 cnzn,
R<|z|<
cnzn,
R<|z|< .
.
a) z называется
устранимой
особой точкой
f(z), если все cn=0
при n>0 f(z)=
называется
устранимой
особой точкой
f(z), если все cn=0
при n>0 f(z)= cnzn,
или $ конечный
предел f(z) при z
cnzn,
или $ конечный
предел f(z) при z
 .
.
b) z называется
полюсом
f(z)
если ряд Лорана функции f(z) в окрестности z
называется
полюсом
f(z)
если ряд Лорана функции f(z) в окрестности z содержит конечное число членов с положительными степенями
f(z)=
содержит конечное число членов с положительными степенями
f(z)=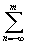 cnzn,
(m>0) или f(z)
cnzn,
(m>0) или f(z)
 при z
при z
 .
.
c) Точка z называется
существенно
особой точкой функции f(z), если ряд Лорана функции f(z) в окрестности
z
называется
существенно
особой точкой функции f(z), если ряд Лорана функции f(z) в окрестности
z содержит
бесконечно много членов с положительными степенями z: f(z)=
содержит
бесконечно много членов с положительными степенями z: f(z)=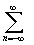 cnzn,
или при z
cnzn,
или при z
 у f(z) нет конечного или бесконечного предела.
у f(z) нет конечного или бесконечного предела.
 17.
Понятие вычета аналитической функции в изолированной особой точке.
17.
Понятие вычета аналитической функции в изолированной особой точке.
Пусть z0-
изолированная особая точка аналитической f(z). f(z)=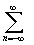 cn(z-z0)n;
0<|z-z0|<r , cn=
cn(z-z0)n;
0<|z-z0|<r , cn= .
.
Определение.
Комплексное число Выч[f(z),z0]=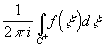 ,
где
С+- замкнутый контур, который
можно стянуть к z0, оставаясь
в кольце аналитичности функции f(z)- называется
вычетом
f(z) в точке z0.
,
где
С+- замкнутый контур, который
можно стянуть к z0, оставаясь
в кольце аналитичности функции f(z)- называется
вычетом
f(z) в точке z0.
Очевидно Выч[f(z),z0]=c-1.
Основная
теорема теории вычетов. Пусть f(z)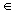 C
C (
(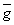 \z1,z2,...,zN)
за
исключением конечного числа N изолированных
особых точек. Тогда
\z1,z2,...,zN)
за
исключением конечного числа N изолированных
особых точек. Тогда  f(z)dz
=2p i
f(z)dz
=2p i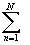 Выч[f(z),zn].
Выч[f(z),zn].
Доказательство. Если
f(z)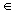 C
C (
(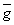 ),
то все точки
),
то все точки 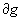 -
правильные
точки f(z). Выделим каждую из изолированных
особых точек zn функции
f(z) замкнутым контуром gn,
не
содержащих внутри других особых точек, кроме zn. В
замкнутой многосвязной области, ограниченной
-
правильные
точки f(z). Выделим каждую из изолированных
особых точек zn функции
f(z) замкнутым контуром gn,
не
содержащих внутри других особых точек, кроме zn. В
замкнутой многосвязной области, ограниченной 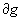 и всеми контурами gn
f(z) является всюду аналитической. По теореме
Коши для многосвязной области
*)
и всеми контурами gn
f(z) является всюду аналитической. По теореме
Коши для многосвязной области
*) f(z)dz+
f(z)dz+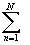
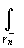 f(z)dz=0.
Перенеся второе слагаемое направо, поменяв направление обхода контуров,
использовав определение вычета *)
получим искомое
f(z)dz=0.
Перенеся второе слагаемое направо, поменяв направление обхода контуров,
использовав определение вычета *)
получим искомое  f(z)dz
=2p i
f(z)dz
=2p i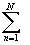 Выч[f(z),zn].
n
Выч[f(z),zn].
n
Как считать
вычеты?
a) z0- устранимая
особая точка *).
Выч[f(z),z0]=0.
b) z0- полюс
порядка m>0 *). f(z)=c-m/(z-z0)m+...+
c-1/z-z0+c0+... =>
=> (z-z0)mf(z)= c-m+...+ c-1(z-z0)m-1+...=>
Выч[f(z),z0]=c-1=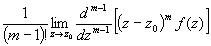 .
.
Частный случай m=1. Выч[f(z),z0]=c-1=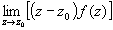 .
.
Если f(z)=j(z)/y
(z), j (z0)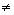 0,
y
(z)=(z-z0) y '(z0)+...;
y
'(z0)
0,
y
(z)=(z-z0) y '(z0)+...;
y
'(z0)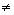 0.
0.
Тогда Выч[f(z),z0]=c-1=j
(z0)/y '(z0).
c) z0- существенно
особая: Выч[f(z),z0]= c-1=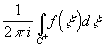
Вычет f(z)
в
z . Выч[f(z),z
. Выч[f(z),z ]=-
]=-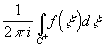 =-c-1. Если
z
=-c-1. Если
z -
устранимая особая точка, то вычет в ней может быть отличен от 0.
-
устранимая особая точка, то вычет в ней может быть отличен от 0.
Пример. f(z)=1+1/z. z - устранимая особая точка, Выч[f(z),z
- устранимая особая точка, Выч[f(z),z ]=
-c-1=-1
]=
-c-1=-1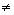 0.
0.
Сумма всех вычетов функции, аналитической
на полной комплексной плоскости, за исключением конечного числа изолированных
особых точек+ z , включая вычет в z
, включая вычет в z равна 0.
равна 0.

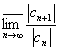 ,
а R2-через {c-n},
n=1,...,
,
а R2-через {c-n},
n=1,..., .
.
 +
+ 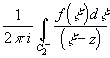 =P(z)+Q(z).
=P(z)+Q(z).
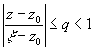 .
Поэтому, дробь 1/(x
-z) можно представить в виде
.
Поэтому, дробь 1/(x
-z) можно представить в виде
 и проведя почленное интегрирование, что возможно в силу равномерной сходимости
ряда по переменной x
на CR (см. доказательство
теоремы Тейлора *)
получим P(z)=
и проведя почленное интегрирование, что возможно в силу равномерной сходимости
ряда по переменной x
на CR (см. доказательство
теоремы Тейлора *)
получим P(z)=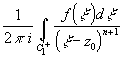 ,
n
,
n .
Поэтому, дробь
.
Поэтому, дробь
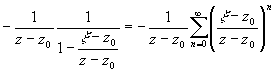 В
результате почленного интегрирования этого ряда получим: Q(z)=
В
результате почленного интегрирования этого ряда получим: Q(z)= .
Изменив направление интегрирования, получим: c-n=
.
Изменив направление интегрирования, получим: c-n=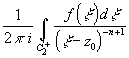 ,
n>0. Подынтегральные функции в выражениях для cn и
c-n являются аналитическими
в круговом кольце R2<|z-z0|<R1.
Поэтому
в силу теоремы Коши *)
значения соответствующих интегралов не изменится при произвольной деформации
контуров интегрирования в области аналитичности подынтегральных функций.
Это позволяет записать общее выражение cn=
,
n>0. Подынтегральные функции в выражениях для cn и
c-n являются аналитическими
в круговом кольце R2<|z-z0|<R1.
Поэтому
в силу теоремы Коши *)
значения соответствующих интегралов не изменится при произвольной деформации
контуров интегрирования в области аналитичности подынтегральных функций.
Это позволяет записать общее выражение cn= ,
n=0,╠ 1, ╠ 2,┘, где
C- произвольный замкнутый контур, лежащий в кольце R2<|z-z0|<R1
и
содержащий точку z0 внутри.
Для f(z) окончательно можно записать: f(z)=
,
n=0,╠ 1, ╠ 2,┘, где
C- произвольный замкнутый контур, лежащий в кольце R2<|z-z0|<R1
и
содержащий точку z0 внутри.
Для f(z) окончательно можно записать: f(z)=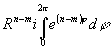 =
= .
.