Степенным рядом назовем ряд вида
Теорема Абеля. Если степенной ряд
Доказательство. В силу необходимого условия сходимости ряда*) $ A>0 : для " n |cn(z1-z0)n|<A =>|cn|<A/|z1-z0|n =>|
![]() 11.
Степенные ряды.
11.
Степенные ряды.
Степенным рядом назовем
ряд вида ![]() cn(z-z0)n,
z0-центр, cn-
коэффициенты заданные комплексные числа. При z= z0
ряд сходится. Это может быть как единственная точка сходимости
cn(z-z0)n,
z0-центр, cn-
коэффициенты заданные комплексные числа. При z= z0
ряд сходится. Это может быть как единственная точка сходимости ![]() n!zn,
а также ряд может сходится на всей комплексной плоскости
n!zn,
а также ряд может сходится на всей комплексной плоскости ![]() zn/n!.
При исследовании степенного ряда важно установить область его равномерной
сходимости. Как будет показано далее, область сходимости степенного ряда
определяется видом его коэффициентов cn.
zn/n!.
При исследовании степенного ряда важно установить область его равномерной
сходимости. Как будет показано далее, область сходимости степенного ряда
определяется видом его коэффициентов cn.
Теорема
Абеля. Если степенной ряд ![]() cn(z-z0)n
сходится в точке z1╧z0,
то он сходится и при "
z: |z-z0|<|z1-z0|,
причем в круге |z-z0|
cn(z-z0)n
сходится в точке z1╧z0,
то он сходится и при "
z: |z-z0|<|z1-z0|,
причем в круге |z-z0|![]() r
<|z1-z0| сходится
равномерно.
r
<|z1-z0| сходится
равномерно.
Доказательство. В силу необходимого условия сходимости ряда*)
$
A>0 : для " n |cn(z1-z0)n|<A
=>|cn|<A/|z1-z0|n
=>|![]() cn(z-z0)n|<A
cn(z-z0)n|<A![]() |(z-z0)/(z1-z0)|n.
По условию теоремы |(z-z0)/(z1-z0)|=q<1=>|
|(z-z0)/(z1-z0)|n.
По условию теоремы |(z-z0)/(z1-z0)|=q<1=>|![]() cn(z-z0)n|<A
cn(z-z0)n|<A![]() qn=>
ряд сходится. При |z-z0|
qn=>
ряд сходится. При |z-z0|![]() r
<|z1-z0| ряд сходится
равномерно по мажорантному признаку Вейерштрасса *)
т.к. |
r
<|z1-z0| ряд сходится
равномерно по мажорантному признаку Вейерштрасса *)
т.к. |![]() cn(z-z0)n|
cn(z-z0)n|![]() A
A![]() |r
/(z1-z0)|n < A
|r
/(z1-z0)|n < A![]() qn
, q<1 n .
qn
, q<1 n .
Следствия теоремы Абеля.
1. Если степенной ряд расходится в
точке z2╧z0,
то он расходится и при "
z: |z-z0|>|z2-z0|.
(Предполагая противное, получим, что по тереме Абеля *)
ряд должен сходится в "
круге радиуса r <|z-z0|,
в частности и в точке z2,
что противоречит условию.).
2. Круг
сходимости.
Радиус сходимости. Рассмотрим sup|z1-z0|=R
для " z1,
где ряд сходится- точную верхнюю грань расстояний от точки z0
до точек z1 в которых сходится
ряд ![]() cn(z-z0)n.
Если R
cn(z-z0)n.
Если R![]()
![]() , то для " z2: |z2-z0|>R
ряд расходится. R=inf|z2-z0|=R
для
, то для " z2: |z2-z0|>R
ряд расходится. R=inf|z2-z0|=R
для
" z2,
где ряд расходится. Пусть R>0, тогда наибольшей областью сходимости
степенного ряда является круг |z-z0|<R
-круг сходимости степенного ряда, число
R>0-
радиус
сходимости степенного ряда.Внутри круга сходимости ряд сходится,
вне- расходится, в точках границы
|z-z0|=R
может как сходиться, так и расходиться.
3.Формула
Коши-Адамара. R=1/L, L=![]()
Доказательство. Пусть 0<L<![]() . Имеем:
. Имеем:
1) Т.к. L=![]() ,
то для
" e>0$
N, что для " n> N
,
то для
" e>0$
N, что для " n> N ![]() <L+e
.
<L+e
.
2) С другой стороны, для того же "e>0
$![]() много членов последовательности {
много членов последовательности {![]() }:
}: ![]() >L-e
.
>L-e
.
Надо доказать:
a) Для "
z1: |z1-z0|<R=1/L
(или что то же самое L|z1-z0|<1)
ряд сходится.
b) Для "
z2: |z2-z0|>R=1/L (L|z1-z0|>1)
ряд расходится.
Докажем это.
a) Возьмем произвольную z1:
L|z1-z0|<1 и выберем
e
=(1-L|z1-z0|)/2|z1-z0|,
тогда
L+e
=(1+L|z1-z0|)/2|z1-z0|.
Т.к. для " n>N:![]() <L+e
=>|z1-z0|
<L+e
=>|z1-z0|![]() <(1-L|z1-z0|)/2=q<1.
=> |cn(z1-z0)n|<qn-
ряд сходится.
<(1-L|z1-z0|)/2=q<1.
=> |cn(z1-z0)n|<qn-
ряд сходится.
b) Выберем e
=(L|z2-z0|-1)/|z2-z0| => L-e
=1/|z2-z0|. Т.к. для![]() числа членов
числа членов ![]() >L-e
=> |z2-z0|
>L-e
=> |z2-z0|![]() >1=>
|cn(z2-z0)n|>1-
ряд расходится. n
>1=>
|cn(z2-z0)n|>1-
ряд расходится. n
Случай L=0: "e>0$
N, что для " n>N ![]() <e
. Положим для "
z и 0<q<1 e =q/|z-z0|
=>|z-z0|
<e
. Положим для "
z и 0<q<1 e =q/|z-z0|
=>|z-z0|![]() <q
=>|cn(z1-z0)n|<qn-
ряд сходится для "
z, т.е R=
<q
=>|cn(z1-z0)n|<qn-
ряд сходится для "
z, т.е R=![]() =1/0=1/L.
=1/0=1/L.
Случай L=![]() :
для " M> 0$
:
для " M> 0$![]() много членов {
много членов {![]() }:
}: ![]() >M.
"e>0$
N, что для
>M.
"e>0$
N, что для
" n>N ![]() <e
. Положим для " z
<e
. Положим для " z![]() z0
и q>1 M=q/|z-z0| =>$
z0
и q>1 M=q/|z-z0| =>$![]() много членов |z-z0|
много членов |z-z0|![]() >1
=>|cn(z1-z0)n|>1-
ряд расходится для " z
>1
=>|cn(z1-z0)n|>1-
ряд расходится для " z![]() z0,
т.е R=0=1/
z0,
т.е R=0=1/![]() =1/L
=1/L
4. В "
круге |z-z0|![]() r
<R степенной ряд сходится равномерно. => По теореме Вейерштрасса
*)
r
<R степенной ряд сходится равномерно. => По теореме Вейерштрасса
*)![]() cn(z-z0)n=f(z)
cn(z-z0)n=f(z)![]() C
C![]() (|z-z0|<R).
(|z-z0|<R).
5. По теореме Вейерштрасса
*)
степенной ряд внутри круга сходимости можно дифференцировать и интегрировать
почленно *)
любое число раз. При этом радиус сходимости не меняется !
6. ![]() cn(z-z0)n=f(z)=>
c0=f(z0),
cn(z-z0)n=f(z)=>
c0=f(z0), ![]() cn+1(n+1)(z-z0)n=f'(z)=>
c1=f'(z0)┘
cn+1(n+1)(z-z0)n=f'(z)=>
c1=f'(z0)┘
![]() cn+k(n+k)!(z-z0)n=f(k)(z)=>
ck=f(k)(z0)/k!
cn+k(n+k)!(z-z0)n=f(k)(z)=>
ck=f(k)(z0)/k!
7. Пример.![]() (z-z0)n
: " cn=1 => R=1. Sn=[1-(z-z0)n+1]/[1-(z-z0)];
|z-z0|<1 и
(z-z0)n
: " cn=1 => R=1. Sn=[1-(z-z0)n+1]/[1-(z-z0)];
|z-z0|<1 и ![]() Sn=1/[1-(z-z0)].
=>
Sn=1/[1-(z-z0)].
=> ![]() (z-z0)n=1/[1-(z-z0)]-
Формула суммы бесконечной геометрической прогрессии.
(z-z0)n=1/[1-(z-z0)]-
Формула суммы бесконечной геометрической прогрессии.
Итак ![]() cn(z-z0)n=>
f(z)
cn(z-z0)n=>
f(z)![]() C
C![]() (|z-z0|<R).
Можно ли функции, аналитической внутри некоторого круга, сопоставить степенной
ряд, сходящийся в этом круге к данной функции?
(|z-z0|<R).
Можно ли функции, аналитической внутри некоторого круга, сопоставить степенной
ряд, сходящийся в этом круге к данной функции?
Ответ на этот
вопрос дает
Теорема Тейлора.
Если f(z)![]() C
C![]() (|z-z0|<R),
то $! степенной
ряд
(|z-z0|<R),
то $! степенной
ряд ![]() cn(z-z0)n
=>f(z) при |z-z0|<R.
cn(z-z0)n
=>f(z) при |z-z0|<R.
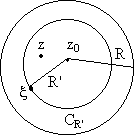 |
Доказательство.
Возьмем " z: |z-z0|<R
и построим CR'
с центром
в точке z0 и содержащую
точку z внутри:
для "xО CR' : |x -z0|=R', R'<R, |x -z0|>|z-z0|. Т.к. f(z) f(z)= |
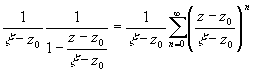 ряд
сходится равномерно по x
на CR'=>f(z)=
ряд
сходится равномерно по x
на CR'=>f(z)=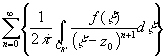 (z-z0)n=
(z-z0)n=cn=![]() =f(n)(z0)/n!,
что и доказывает $
и единственность разложения. n
=f(n)(z0)/n!,
что и доказывает $
и единственность разложения. n
Замечания. 1)
Разложение функции f(z)=![]() cn(z-z0)n
называют
разложением
функции в ряд Тейлора.
cn(z-z0)n
называют
разложением
функции в ряд Тейлора.
2) По теореме Коши *)
cn=![]() ,
где C- произвольный кусочно-гладкий контур, содержащий внутри себя точку
z0.
,
где C- произвольный кусочно-гладкий контур, содержащий внутри себя точку
z0.
![]() 12.
Единственность определения аналитической функции.
12.
Единственность определения аналитической функции.
п.1. Понятие
правильной точки.
Пусть f(z) задана в g, за исключением
может быть некоторых изолированных точек.
Точка z0![]() g
называется правильной точкой функции f(z),
заданной в g, если $
g
называется правильной точкой функции f(z),
заданной в g, если $![]() cn(z-z0)n=f(z)
в g
cn(z-z0)n=f(z)
в g![]() |z-z0|
<r (z0),
где r (z0)-радиус
сходимости степенного ряда. *)
|z-z0|
<r (z0),
где r (z0)-радиус
сходимости степенного ряда. *)
Все остальные точки z![]() g-
особые
точки функции f(z), заданной в g.
g-
особые
точки функции f(z), заданной в g.
Замечание. Если f(z)![]() C
C![]() (g),
то все z
(g),
то все z![]() g- правильные
точки
f(z). Если f(z) задана в
g- правильные
точки
f(z). Если f(z) задана в ![]() ,
то граничные точки могут быть как правильными, так и особыми.
,
то граничные точки могут быть как правильными, так и особыми.
п.2. Нули аналитической
функции.
Пусть f(z)![]() C
C![]() (g);
f(z0)=0, z0
(g);
f(z0)=0, z0![]() g,
тогда z0 - нуль аналитической
функции. f(z)=
g,
тогда z0 - нуль аналитической
функции. f(z)=![]() cn(z-z0)n
=> c0=0. Если c1=┘=
cn-1=0, а cn
cn(z-z0)n
=> c0=0. Если c1=┘=
cn-1=0, а cn![]() 0,
то z0 - нуль n-того
порядка.
0,
то z0 - нуль n-того
порядка.
Заметим, что в нуле n-того порядка f(z0)=f'(z0)=┘
f(n-1)(z0)=0, f(n)(z0)![]() 0
и f(z)=(z-z0)n f1(z), f1(z0)
0
и f(z)=(z-z0)n f1(z), f1(z0)![]() 0.
0.
Теорема
о нулях аналитической функции.
Пусть f(z)![]() C
C![]() (g)
и обращается в 0 в бесконечном множестве различных точек
(g)
и обращается в 0 в бесконечном множестве различных точек
(zi![]() zk,
все zn
zk,
все zn![]() g
и f(zn)=0), имеющем предельную
точку (точку сгущения) z*
g
и f(zn)=0), имеющем предельную
точку (точку сгущения) z*![]() g
g
(![]() zn=z*
zn=z*![]() g).
Тогда f(z)
g).
Тогда f(z)![]() 0, для z
0, для z![]() g.
g.
Доказательство. По непрерывности
f(z*)=0 => f(z)=![]() cn(z-z*)n,
где |z-z*|<r (z*)
=> c0=0, и f(z)=(z-z*)f1(z);
f1(z)=
cn(z-z*)n,
где |z-z*|<r (z*)
=> c0=0, и f(z)=(z-z*)f1(z);
f1(z)= ![]() cn(z-z*)n;
f1(zn)=0=> по непрерывности
f1(z*)=0 => c1=0
и так далее => cn=0 для
"
n. Итак f(z)
cn(z-z*)n;
f1(zn)=0=> по непрерывности
f1(z*)=0 => c1=0
и так далее => cn=0 для
"
n. Итак f(z)![]() 0 в круге |z-z*|
<r (z*),
где r (z*)
не меньше, чем расстояние от z*
до
0 в круге |z-z*|
<r (z*),
где r (z*)
не меньше, чем расстояние от z*
до ![]() . Тождественное
равенство f(z)
. Тождественное
равенство f(z)![]() 0 во всей области g
доказывается аналогично доказательству принципа максимума
*)
0 во всей области g
доказывается аналогично доказательству принципа максимума
*)
Достаточно показать, что f(z**)=0,
где z**![]() g
- произвольная точка, лежащая вне круга |z-z*|
<r (z*).
Соединим z* и z**
спрямляемой
кривой L, целиком лежащей в g и отстоящей от
g
- произвольная точка, лежащая вне круга |z-z*|
<r (z*).
Соединим z* и z**
спрямляемой
кривой L, целиком лежащей в g и отстоящей от ![]() на расстояние d>0. Поскольку "
точку круга |z-z*|<r (z*),
лежащую внутри g можно рассматривать как предел последовательности нулей
функции f(z), то выбрав в качестве нового центра разложения последнюю точку
z=z1 пересечения кривой
L с окружностью |z-z*|=r (z*),
получим, что f(z)
на расстояние d>0. Поскольку "
точку круга |z-z*|<r (z*),
лежащую внутри g можно рассматривать как предел последовательности нулей
функции f(z), то выбрав в качестве нового центра разложения последнюю точку
z=z1 пересечения кривой
L с окружностью |z-z*|=r (z*),
получим, что f(z)![]() 0 внутри круга |z-z1|<r
(z1), где
0 внутри круга |z-z1|<r
(z1), где
r (z1)![]() d.
Продолжая этот процесс, покроем кривую L конечным числом кругов, радиусов
не меньше d, внутри которых f(z)
d.
Продолжая этот процесс, покроем кривую L конечным числом кругов, радиусов
не меньше d, внутри которых f(z)![]() 0.
При этом точка z=z** попадет
внутрь последнего круга => f(z**)
0.
При этом точка z=z** попадет
внутрь последнего круга => f(z**)![]() 0. В силу произвольности z** => f(z)
0. В силу произвольности z** => f(z)![]() 0
в g.n
0
в g.n
Следствия.
1. Все нули f(z)![]() C
C![]() (g)
и f(z) тождественно
(g)
и f(z) тождественно ![]() 0 в g -
изолированные.
0 в g -
изолированные.
2. Если f(z)![]() C
C![]() (g)
и f(z) тождественно
(g)
и f(z) тождественно ![]() 0 в g, то
в " ограниченной
0 в g, то
в " ограниченной ![]() '
'![]() g может быть лишь конечное число нулей f(z).
g может быть лишь конечное число нулей f(z).
Доказательство Если множество
нулей в ![]() '- бесконечно,
то из него можно выделить пооследовательность, сходящуюся к z
'- бесконечно,
то из него можно выделить пооследовательность, сходящуюся к z![]()
![]() '
=>f(z)
'
=>f(z)![]() 0
в g, что противоречит условию. n
0
в g, что противоречит условию. n
2. Если f(z)- целая
*),
то в " ограниченной![]() '
может быть лишь конечное число нулей f(z). На расширенной комплексной плоскости
*)
целая функция может иметь лишь счетное число нулей, причем предельноой
точкой этого множества является бесконечно удаленная точка *)
.
'
может быть лишь конечное число нулей f(z). На расширенной комплексной плоскости
*)
целая функция может иметь лишь счетное число нулей, причем предельноой
точкой этого множества является бесконечно удаленная точка *)
.
п.3. Теорема
единственности определенной аналитической функции.
Теорема.
Если f1(z) и f2(z)![]() C
C![]() (g)
и $ {zn}
(g)
и $ {zn}![]() z*
z*![]() g,
zi
g,
zi![]() zk и
f1(zn)=f2(zn),
то f1(z)
zk и
f1(zn)=f2(zn),
то f1(z)![]() f2(z)
для " z
f2(z)
для " z![]() g.
g.
Для доказательства достаточно при помощи
теоремы о нулях *)
установить, что функция h(z)=f1(z)-f2(z)![]() 0
в g.
0
в g.
Следствия теоремы единственности.
Множество задания аналитической функции.
В области g может существовать
только
одна аналитическая функция, принимающая заданные значения на
a) {zn}![]() z*
z*![]() g,
zi
g,
zi![]() zk
zk
b) x![]() C
C![]() g,
C- кусочно-гладкая кривая.
g,
C- кусочно-гладкая кривая.
c) z![]()
![]() '
'![]() g.
g.
Другими словами: Функция аналитическая
в g
однозначно
определяется заданием своих значений
на a), b), c).
Существенное замечание. Может -
не значит существует. Нельзя произвольно задавать значения f(zn)
или f(C) или f(![]() ')
!
')
!