Лекция 7.
 13.
Понятие аналитического продолжения.
13.
Понятие аналитического продолжения.
п.1. Аналитическое
продолжение через общую подобласть двух областей.
Пусть f1(z) C
C (g1)
и g1
(g1)
и g1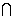 g2=g12
g2=g12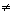
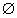 и
пусть f2(z)
и
пусть f2(z) C
C (g2),
причем f2(z)
(g2),
причем f2(z)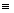 f1(z),
z
f1(z),
z g12.
Тогда f2(z) называется аналитическим
продолжением f1(z)
на g2 через общую подобласть
g12.
g12.
Тогда f2(z) называется аналитическим
продолжением f1(z)
на g2 через общую подобласть
g12.
В силу теоремы единственности определенной
аналитической функции *)
если аналитическое продолжение $
, то оно- единственно. При этом в g=g1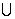 g2
$!
(единственная) аналитическая функция F(z)=
g2
$!
(единственная) аналитическая функция F(z)=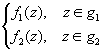
 C
C (g). F(z) называется аналитическим продолжением своего первоначального
элемента f1(z)
(g). F(z) называется аналитическим продолжением своего первоначального
элемента f1(z) C
C (g1)
на большую область g, для которой g1
(g1)
на большую область g, для которой g1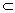 g
√ подобласть.
g
√ подобласть.
Осуществить аналитическое продолжение
можно с помощью степенных рядов. Пусть f(z) C
C (g)
и z0
(g)
и z0 g-
правильная точка g, т.е. $
g-
правильная точка g, т.е. $ 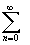 cn(z-z0)n
сходящийся к f(z) в общей части g и круга сходимости степенного ряда |z-z0|
<r (z0).
Если r (z0)
больше расстояния от точки z0 до
cn(z-z0)n
сходящийся к f(z) в общей части g и круга сходимости степенного ряда |z-z0|
<r (z0).
Если r (z0)
больше расстояния от точки z0 до ,
то круг сходимости выйдет за пределы g, и мы получим F(z)- аналитическое
продолжение f(z)
,
то круг сходимости выйдет за пределы g, и мы получим F(z)- аналитическое
продолжение f(z) C
C (g)
на большую область g
(g)
на большую область g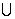 |z-z0|<r
(z0).
|z-z0|<r
(z0).
п.2. Важная
теорема.
Теорема 13.1
На границе круга сходимости
*)
степенного ряда найдется хотя бы одна особая *)
точка аналитической функции комплексной переменной, которая (функция) является
суммой ряда внутри его круга сходимости |z-z0|<R0.
Доказательство (от противного).
Предположим, что " x
: |x -z0|=R0
являются правильными *)
точками f(z)=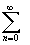 cn(z-z0)n,
f(z)
cn(z-z0)n,
f(z) C
C (|z-z0|
<R0) т.е. для "x
(|z-z0|
<R0) т.е. для "x
$ r (x)>0: 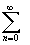 cn(x)(z-x)n=f(z)
в общей части |z-z0| <R0
cn(x)(z-x)n=f(z)
в общей части |z-z0| <R0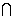 |x
-z0|<r (x).
|x
-z0|<r (x).
Докажем, что r
(x )>0 является
непрерывной функцией x
на CR0 и даже
Липшиц-
непрерывной: т.е. |r (x1)-r(x2)| |x 1-x2|.
|x 1-x2|.
Предположим противное. Пусть r
(x1)>r(x2)
и $ d>0 : r
(x1)>r(x2)+|x1-x2|+d
(*).
Это
означает, что круг |z-x2|<r
(x2)
лежит внутри круга |z-x1|<r
(x1).
Но в общей части трех кругов |z-z0|<R0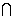 |z-x1|<r(x1) |z-x1|<r(x1)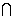 |z-x2|<r(x2)
все три степенных ряда сходятся к одной и той же f(z) |z-x2|<r(x2)
все три степенных ряда сходятся к одной и той же f(z) C C (|z-z0|<R0)
=>степенной ряд
(|z-z0|<R0)
=>степенной ряд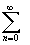 cn(x2)(z-x2)n
может
быть продолжен на большую область, т.е. он сходится в круге cn(x2)(z-x2)n
может
быть продолжен на большую область, т.е. он сходится в круге |
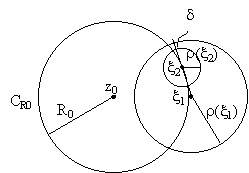 |
радиуса r
(x2),
который не меньше чем расстояние от x2
до границы круга |z-x1|<r
(x1) => r
(x2) r
(x1)-|x1-x2|,
но тогда из (*) =>r
(x1)>r
(x1)+d и
т.к. d>0
мы пришли к абсурдному заключению. Но это противоречие явилось следствием
нашего предположения о том, что r (x
) не является Липшиц- непрерывной *)
на CR0. Итак: |r
(x1)-r
(x2)|
r
(x1)-|x1-x2|,
но тогда из (*) =>r
(x1)>r
(x1)+d и
т.к. d>0
мы пришли к абсурдному заключению. Но это противоречие явилось следствием
нашего предположения о том, что r (x
) не является Липшиц- непрерывной *)
на CR0. Итак: |r
(x1)-r
(x2)| |x 1-x2|.
|x 1-x2|.
Из Липшиц- непрерывности => простая непрерывность.
А т.к. непрерывная функция r (x
)>0 на замкнутом множестве |x -z0|=R0
достигает своей нижней грани, т.е. $x*
:
r (x ) r
(x*)
для "x
r
(x*)
для "x CR0.
Но по предположению для "x
CR0.
Но по предположению для "x CR0
r (x )>0 =>r
(x*)=r0>0.
Из того, что r (x
)
CR0
r (x )>0 =>r
(x*)=r0>0.
Из того, что r (x
) r0
следует,
что функция f(z)=
r0
следует,
что функция f(z)=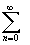 cn(z-z0)n
при | z-z0|<R0
может быть аналитически продолжена в круг |z-z0|<R0+r0,
а следовательно, радиус сходимости исходного степенного ряда не R0,
а R0+r0.
Но это противоречит условиям теоремы.
cn(z-z0)n
при | z-z0|<R0
может быть аналитически продолжена в круг |z-z0|<R0+r0,
а следовательно, радиус сходимости исходного степенного ряда не R0,
а R0+r0.
Но это противоречит условиям теоремы.
К этому противоречию мы пришли, предположив,
что все точки x CR0-
правильные. => На CR0 имеется
хотя бы одна точка x**,
являющаяся особой, т.е. r (x**)=0.
n
CR0-
правильные. => На CR0 имеется
хотя бы одна точка x**,
являющаяся особой, т.е. r (x**)=0.
n
Следствие.
Радиус круга сходимости определяется расстоянием от центра сходимости до
ближайшей особой точки той аналитической функции, к которой сходится данный
ряд.
Примеры.
1. 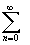 (-1)nz2n=
(-1)nz2n=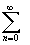 (-z2)n=1/(1+z2);
|z|<1.
(-z2)n=1/(1+z2);
|z|<1.
Особые точки суммы ряда очевидно z1,2=╠
i. Отсюда понятно, почему разложение функции f(x)= 1/(1+x2)
в степенной ряд в окрестности точки x=0 абсолютно сходится только при -1<x<1,
условно сходится при |x|=1 и расходится при |x|>1, хотя эта функция при
"
x обладает непрерывными и ограниченными производными "
порядка.
2. Степенной ряд, сумма
которого имеет счетное, всюду плотное множество особых точек на границе
своего круга сходимости.
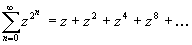 -
сходится при |z|<1 (по формуле Коши- Адамара *).
-
сходится при |z|<1 (по формуле Коши- Адамара *).
При z=1 ряд расходится. Рассмотрим точки 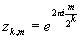 ,
|zk,m|=1; k-фиксировано, m=0,1,2....;
m=0, zk,0=1; m=2k ,
,
|zk,m|=1; k-фиксировано, m=0,1,2....;
m=0, zk,0=1; m=2k , 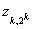 =1,
при m=1,... ,2k-1 точки
делят окружность единичного радиуса на 2k
частей.
=1,
при m=1,... ,2k-1 точки
делят окружность единичного радиуса на 2k
частей.
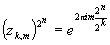 и
при n
и
при n k
k 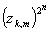 =1=>
в этих точках ряд расходится.
=1=>
в этих точках ряд расходится.
При k
 точки zk,m всюду плотно
расположены на единичной окружности
точки zk,m всюду плотно
расположены на единичной окружности
Таким образом, сумма ряда имеет
счетное, всюду плотное множество особых точек на границе единичного круга
=> Эту аналитическую функцию нельзя аналитически продолжить за границу
единичного круга !!. (Т.к. в "
z: |z|<1 радиус круга сходимости степенного ряда будет не больше расстояния
до границы единичного круга. По следствию к теореме 13.1 *)
п.3. Аналитическое
продолжение через общий участок границы двух областей.
Теорема 13.2
Пусть fi(z) C
C (gi),
i=1,2 и fi(z)
(gi),
i=1,2 и fi(z) C
C (gi+G
) и f1|G
= f2|G
. Тогда F(z)=
(gi+G
) и f1|G
= f2|G
. Тогда F(z)=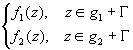
 C
C (g=g1+g2+G
).
(g=g1+g2+G
).
Доказательство. Достаточно
показать, что " z0 Gявляется
правильной точкой F(z) (кроме может быть концевых точек G
). Возьмем " z0
Gявляется
правильной точкой F(z) (кроме может быть концевых точек G
). Возьмем " z0 G
и
построим
G
и
построим
C=C1(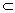 g1)+C2(
g1)+C2(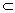 g2);
C
g2);
C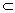 g-
кусочно- гладкие. Рассмотрим интеграл типа Коши *)
g-
кусочно- гладкие. Рассмотрим интеграл типа Коши *)
F (z)=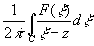  C C (g' (g'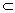 g).
Поскольку при z g).
Поскольку при z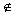 C F
(z) непрерывна на C, то z0-
правильная точка F (z).
Пусть C F
(z) непрерывна на C, то z0-
правильная точка F (z).
Пусть
z1 g'1.
Тогда F (z1)= g'1.
Тогда F (z1)=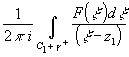 + +
+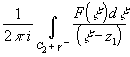 .
Второе слагаемое равно 0 т.к. z1 .
Второе слагаемое равно 0 т.к. z1 g'1.
=> F (z1)=F(z1). g'1.
=> F (z1)=F(z1). |
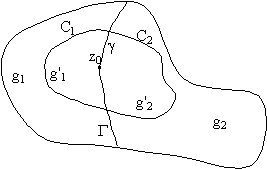 |
Аналогично получим, что при z2 g'2
F (z2)=F(z2).
По непрерывности получим, что F(z0)=F
(z0) => z0
g'2
F (z2)=F(z2).
По непрерывности получим, что F(z0)=F
(z0) => z0 G
является правильной точкой F(z).
n
G
является правильной точкой F(z).
n
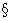 14.
Аналитическое продолжение с действительной оси.
14.
Аналитическое продолжение с действительной оси.
Элементарные функции комплексной переменной.
Пусть отрезок [a,b]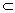 области g комплексной плоскости z. Тогда в силу теоремы единственности
определенной аналитической функции *)
в g может $ !
функция
области g комплексной плоскости z. Тогда в силу теоремы единственности
определенной аналитической функции *)
в g может $ !
функция
f(z) C
C (g),
принимающая заданные значения f(x) на x
(g),
принимающая заданные значения f(x) на x [a,b].
Если такая f(z) $
, то она называется аналитическим
продолжением в комплексную плоскость функции действительной переменной,
заданной на действительной оси. f(x)- вообще говоря, комплексная
функция действительной переменной. Причем в силу свойств аналитической
функции f(x) должна быть бесконечно дифференцируема по x !!.
[a,b].
Если такая f(z) $
, то она называется аналитическим
продолжением в комплексную плоскость функции действительной переменной,
заданной на действительной оси. f(x)- вообще говоря, комплексная
функция действительной переменной. Причем в силу свойств аналитической
функции f(x) должна быть бесконечно дифференцируема по x !!.
Элементарные функции действительной переменной.
sin x= 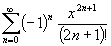 ;
cos x=
;
cos x=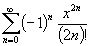 ; ex=
; ex=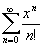 ;
;
Целые функции *)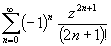 ,
, 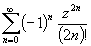 ,
, 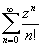 -
единственные аналитические продолжения sin x, cos x, ex
на всю комплексную плоскость z. Естественно сохранить для них старые обозначения.
Прямой проверкой проверяется формула
Эйлера:
-
единственные аналитические продолжения sin x, cos x, ex
на всю комплексную плоскость z. Естественно сохранить для них старые обозначения.
Прямой проверкой проверяется формула
Эйлера:
eiz=cos z+ isin z. Однако,
это, с одной стороны требует нудных преобразований и обоснования возможности
перестановки членов абсолютно сходящихся рядов, а с другой стороны, является
следствием общего положения и возможности аналитического продолжения не
только функций, но и аналитических соотношений.
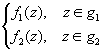
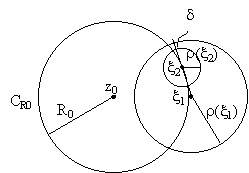
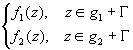
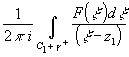 +
+
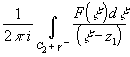 .
Второе слагаемое равно 0 т.к. z1
.
Второе слагаемое равно 0 т.к. z1