п.5. Связь аналитической функции комплексной переменной .и гармонической функции двух действительных переменных.
f(z)=u(x,y)+iv(x,y)C(g). =>u_x=v_y; u_y=-v_x;
=> D u=0; D v=0; -гармонические функции (x,y)g.
Обратно, пара гармонических в g функций u(x,y) и v(x,y), связанные условиями Коши- Римана, являются действительной и мнимой частью аналитической функции.
п.6. Сохранение оператора Лапласа при конформном отображении.
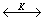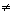Пусть (x,y)g и f(z)=z : gD; z =x (x,y)+ih (x,y)C(g); (x ,h )D; f'(z)0.
D _xyu=?
u_xx=u_xxx_x²+2u_xhx_xh _x+u_{h h}h_x²+u_xx_xx+u_hh_xx
u_yy=u_xxx_y²+2u_xhx_yh _y+u_hh h_y²+u_xx_yy+u_hh_yy
D _xyu= u_xx(x_x²+x_y²)+ 2u_xh(x_xh _x+x _yh _y)+u_{h h}(h_x²+h_y²)+u_x(x_xx+x_yy)+u_h (h_xx+h_yy)=
={x _x=h_y, x_y=-h_x,=> f'(z)=x_x+ih_x=x_x-ix_y=h_y+ih_x=>|f'(z)|²=x_x²+x_y²=h_x²+h_y²;
x_xh _x+x _yh _y=x _xx+x_yy =(h _xx+h_yy)=0}=|f'(z)|²D_xhu(x ,h )={z=j (z )}=[1/|j '(z )|²] D_xhu(x ,h )

п.7. Применение конформных отображений в задачах электростатики.
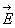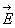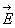{rot=0; div =4pr ; =-С u =>D u=-4pr .

Задача Робэна- распределение заряда на проводящей границе.
 

q=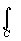s (s)ds-дано; s (s)=(1/4p )En|C=-(1/4p )╤ u/╤ n|C; n-внешняя нормаль. Задача Робэна: D u=0 вне С;. u|C=const; 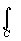 ╤ u/╤ n ds=-4p q - дано.   Найти s (s)=?

Задача просто решается, если С есть окружность |z |=1.
Тогда W (s)=q/2p =-(1/4p )╤ u₀/╤ n₀. =>╤ u₀/╤ n₀|_{|z |=1}=-2q.
Пусть известна функция z =f(z), которая конформно отображает С на плоскости z на окружность |z |=1 на плоскости z .
Тогда ╤ u/╤ n|_C=╤ u₀/╤ n₀|_{|z |=1} ╤ n₀/╤ n|_C+╤ u₀/╤t₀|_{|z |=1} ╤t ₀/╤ n|_C = (поскольку контур проводящий, то E_t =╤ u₀/╤t ₀=0) =-2q ╤ n₀/╤ n|_C;
Но при конформном отображении нормаль n к С переходит в нормаль n₀ к |z |=1, а меняется лишь ее длина => ╤ n₀/╤ n|_C=|f'(z)|_C=> ╤ u/╤ n|_C=-2q |f'(z)|_C .
=> s(s)= (q/2p) |f'(z)|_C .
 

Пример. Двусторонний отрезок [-1;1] на плоскости z . z =f(z): C|z |=1- функция,

обратная к функции Жуковского z =f(z)=;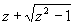

 
f'(z)|_{zО [-1;1]}=1+z/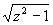|_{zО [-1;1]}=f(z)/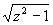 |_{zО [-1;1]}
Но |f(z)|_{zО [-1;1]}=|z |=1=>|f'(z)|_{zО [-1;1]}=1/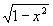;-1<x<1;=>s(x)=q/[2p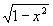];-1<x<1;
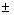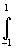Замечания. 1) s (x), x1- эффект острия; 2) 2s (x)dx=q (Двусторонний отрезок).

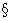21. Основные понятия операционного исчисления.
Операционное исчисление - это аппарат интегральных преобразований, позволяющий заменить операции дифференцирования и интегрирования функции действительной переменной (известной или неизвестной, заданной или искомой) на алгебраические операции с параметрами интегральных преобразований.
п.1. Понятие одностороннего преобразования Лапласа.
Класс рассматриваемых функций действительной переменной. f(t), -<t<
1)    f(t)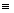0, t<0
2)    f(t)- кусочно- непрерывна при t>0, т.е. для " конечного [a,b]  f(t) имеет лишь конечное число разрывов I рода.
$ M>0, a'>0 : |f(t)|<Me^a't, t╝ (f(t)-функция ограниченной степени роста).
inf a'=a- показатель степени роста.

Класс А(а)- класс функций ограниченной степени роста.
Замечания
1.    Для f(t)=tⁿА(0), a=0, т.к. tⁿ<Me^a't для " a'>0.
2.    f(t)=exp(2t²)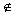А(а) для " a.
Определение. Односторонним преобразованием Лапласа функции f(t) класса А(а) называется функция комплексной переменной F(p), определяемая соотношением 
F(p)=e^-ptf(t)dt;
Если $ F(p), то f(t)F(p); f(t)-оригинал, F(p)-изображение.
Для каких p $ F(p) ?
Теорема 21.1 Если f(t)A(a), то F(p) $ при Re p>a и в области Re px₀>a интеграл сходится равномерно по р.
Доказательство. Возьмем для " x>a; Re p=x>a'>a. Очевидно, |f(t)|<Me^a't. Рассмотрим |e^-ptf(t)dt|<Me^-xte^a'tdt=M/(x-a') => при Re p=x>a' $ F(p). Существование доказано. Для доказательства равномерной сходимости интеграла по параметру р в области 
Re px₀>a можно воспользоваться достаточным мажорантным признаком Вейерштрасса. Т.к. |f(t)|<Me^a't, x₀>a'>a, то |e^-ptf(t)|<Me^-(x0-a')t всюду в области Re px₀>a, причем мажоранта не зависит от р. n
Замечание. Вспомогательный параметр a' нам потребовался для доказательства, чтобы включить в рассмотрение функции класса А(0).
Каковы аналитические свойства F(p)?
Теорема 21.2. В области Rep>a (f(t)A(a)) F(p)C(Re p>a).
Доказательство. 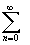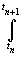e^-ptf(t)dt=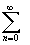u_n(p); u_n(p)-целые *) функции; 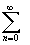u_n(p).=>F(p), 
Re px₀>a; по теореме Вейерштрасса *) => F(p)C(Re p>a). n
Замечание. Т.к. 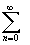u^(k)_n(p).=>F^(k)(p)   Re px₀>a, то F^(k)(p)=(-1)^ke^-ptf(t)t^kdt !
п.2. Свойства изображений.
1.    f(t)=s (t)={0, t<0; 1, t>0; s (t)- функция Хевисайда. s (t) А(0) =>
=>F(p)C(Re p>0); F(p)=e^-ptdt=1/p; s (t) 1/p, Re p>0.
2.    f(t)=tⁿ ; n >-1; tⁿ А(0); F(p)C(Re p>0); F(p)=tⁿ e^-ptdt; F(x>0)=tⁿ e^-xtdt= 
= {xt=s}=(1/x^{n +1})sⁿ e^-sds=G (n +1)/x^{n +1}; F(p)- аналитическое продолжение F(x) в правую полуплоскость Re p>0; =>F(p)=G (n +1)/p^{n +1}; Если n -дробное, то берется та ветвь корня, которая является непосредственным аналитическим продолжением 
x^{n +1}, x>0. Частный случай n =0; f(t)=s (t)1/p, Re p>0. При n =n : tⁿn!/pⁿ⁺¹
3.    f(t)=e^{a t}; Re p> Re a ; F(p)=e^{a t} e^-ptdt=1/(p-a ); Re p> Re a ;