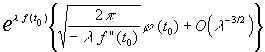Лекция 14.
 22.
Метод перевала.
22.
Метод перевала.
Метод вычисления асимптотических разложений
интегралов по кривой на комплексной плоскости аналитических функций комплексной
переменной, зависящих от действительного параметра.
F(l )=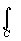 elf(z)j(z)dz;
l
>>1.
elf(z)j(z)dz;
l
>>1.
Как Вы знаете из курса анализа- асимптотическое
разложение функции f(x) в окрестности точки x0
имеет вид:
f(x)=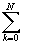 jk(x)+RN+1(x);
jk+1(x)=o(jk(x));
RN+1(x)=o(jN(x)).
jk(x)+RN+1(x);
jk+1(x)=o(jk(x));
RN+1(x)=o(jN(x)).
При x0
 достаточно часто в качестве j
(x) выбираются обратные степени x:
достаточно часто в качестве j
(x) выбираются обратные степени x:
f(x)=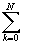 сk/xk+RN+1(x);
RN+1(x)=o(1/xN) и часто
RN+1(x)=сN+1/xN+1.
сk/xk+RN+1(x);
RN+1(x)=o(1/xN) и часто
RN+1(x)=сN+1/xN+1.
Замечание. Асимптотический
ряд, вообще говоря, не сходится.
В курсе анализа был рассмотрен метод асимптотических разложений
F(l )=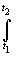 elf(t)j(t)dt;
l>>1,
elf(t)j(t)dt;
l>>1,
и для достаточно гладких f(t) иj(t)
при условии существования единственного глобального максимума f(t)
на [t1;t2] : f(t0)>f(t), f'(t0)=0,
f"(t0)<0
была получена формула Лапласа:
F(l
)=.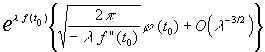
Обобщим этот результат на случай интегралов
от аналитических функций комплексной переменной.
F(l )=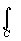 elf(z)j(z)dz;
l
>>1, C
elf(z)j(z)dz;
l
>>1, C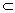 g, f(z),
j(z)
g, f(z),
j(z) C
C (g).
(g).
Пусть f(z)=u(x,y)+iv(x,y); |eil
v(x,y)|=1; и эта часть экспоненты- только
осциллирующая подынтегральная функция. Очевидно, наибольший вклад в интеграл
даст тот участок кривой интегрирования, на котором u(x,y) достигает глобального
максимума на С.
Пусть z0-
единственная точка глобального максимума u(x,y) на С: u(x0,y0)>u(x,y)|C.
Как ведет себя функция u(x,y) в окрестности
этой точки ?
D u=0, z g',
и в силу принципа максимума гармонической функции,
g',
и в силу принципа максимума гармонической функции,
max u|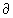 g>u(x,y)|(x,y)
g>u(x,y)|(x,y) g'=>
хотя z0
g'=>
хотя z0 С
точка глобального максимума u(x,y) на С, но в окрестности точки z0
в g' найдутся точки не лежащие на С, в которых значения u(x,y)>u(x0,y0)=>
Через z0
С
точка глобального максимума u(x,y) на С, но в окрестности точки z0
в g' найдутся точки не лежащие на С, в которых значения u(x,y)>u(x0,y0)=>
Через z0 С
проходят другие кривые (направления) на которых u(x,y) возрастает от значения
u(x0,y0). Точка
z0=x0+iy0 - седловая
точка, или точка перевала поверхности u(x,y). Отсюда
и название метода.
С
проходят другие кривые (направления) на которых u(x,y) возрастает от значения
u(x0,y0). Точка
z0=x0+iy0 - седловая
точка, или точка перевала поверхности u(x,y). Отсюда
и название метода.
Очевидно, наибольший вклад в интеграл будет давать участок интегрирования
в окрестности точки z0, если на
нем u(x,y) будет убывать с наибольшей скоростью от значения u(x0,y0).
В силу теоремы Коши *)
контур интегрирования С в окрестности точки z0 С
можно деформироовать как угодно, не меняя значения интеграла.
С
можно деформироовать как угодно, не меняя значения интеграла.
В частности, участок контура С, проходящий
через z0 можно направить
по направлению наибыстрейшего спуска на поверхности u(x,y). Это
направление определяется направлением 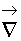 u
(grad u) в точке z0 .
Но (
u
(grad u) в точке z0 .
Но (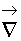 u,
u,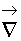 v) =uxvx+uyvy=0
v) =uxvx+uyvy=0
(в силу условий Коши-Римана *).
=> Направлением наибыстрейшего спуска будет
направление 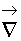 v=0, т.е линия уровня v(x,y)=v(x0,y0)=const.
v=0, т.е линия уровня v(x,y)=v(x0,y0)=const.
Итак, Наибольший вклад в
интеграл дает интегрирование по участку С, проходящему через z0
и совпадающему с линией уровня v(x,y)=v(x0,y0)=const.
Как ведет себя f(z) на этом участке?
f't(z)=ut(x,y)|C+ivt
(x,y)|C, но vt(x,y)|C=0
и ut(x0,y0)|C=0,
т.к. z0- точка глобального
максимума и на С=> f'(z0)=0 (производная
не зависит от направления).
vtt |C=0 (т.к.
v(x,y)=v(x0,y0)=const),
utt(z0)<0 => f''(z0)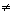 0.
0.
Найдем направление наибыстрейшего спуска.
f(z)=f(z0)+(1/2)f''(z0)(z-z0)2+O(|z-z0|3);
(1/2)f''(z0)=keiy, z-z0=reiq,
u(x,y)=u(x0,y0)+kr2cos(y
+2q )+O(r3); v(x,y)=v(x0,y0)+kr2sin(y
+2q )+O(r3);
При 0 q
q 2p
cos(y +2q )
4 раза обращается в 0 => окрестность
точки
z0 разбивается на
4 сектора- два положительных: cos(y+2q
)>0, и два отрицательных: cos(y
+2q )<0.
2p
cos(y +2q )
4 раза обращается в 0 => окрестность
точки
z0 разбивается на
4 сектора- два положительных: cos(y+2q
)>0, и два отрицательных: cos(y
+2q )<0.
Кривая С должна в точке z0
переходить из одного отрицательного сектора в другой.
Направление наибыстрейшего спуска определяется
условием cos(y +2q
)=-1 =>
y +2q0=p;
q0=(p
-y )/2, где
f''(z0)=2keiy.
Перейдем теперь к вычислению первого члена
асимптотики интеграла.
F(l )=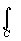 elf(z)j(z)dz=
eil v(z0)
elf(z)j(z)dz=
eil v(z0)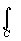 elu(z)j(z)dz,
v(x,y)|C=const.
elu(z)j(z)dz,
v(x,y)|C=const.
Параметризуем контур интегрирования С:
z=z(t),
z0=z(0);
F1(l )=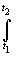 elU(t)F(t)(dz/dt)dt;
F(t)=j(z(t));
U(t)=u(x(t),y(t)), U(0)>U(t), U'(0)=0;
elU(t)F(t)(dz/dt)dt;
F(t)=j(z(t));
U(t)=u(x(t),y(t)), U(0)>U(t), U'(0)=0;
Выполнены все условия применимости формулы
Лапласа.
F1(l )=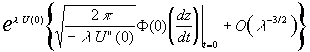 ;
U(0)=u(x0,y0); F (0)=j
(z0);
;
U(0)=u(x0,y0); F (0)=j
(z0);
Т.к. V(t)|C=const=> V"(t)|C=0; => U"(0)= d2/dt2
[f(z(t))]|t=0 =d/dt [f'(z) dz/dt]|t=0 =
=[f"(z) (dz/dt)2]|t=0+[f'(z)d2z/dt2]|t=0
=={f'(z0)=0}=f"(z0)[(dz/dt)2]|t=0.
Осталось найти [(dz/dt)2]|t=0.
z=z0+teiq 0, 2q0=p-y;
=> [(dz/dt)]|t=0=eiq 0;
|(dz/dt)||t=0=1 => [(dz/dt)2]|t=0= ei2q
0;
а т.к. f"(z0)=2keiy=>
U"(0)=f"(z0)[(dz/dt)2]|t=0= 2keiyei2q
0=2kei(y +2q
0)=2keip= -2k= -|f"(z0)|.
=>
=> F(l )=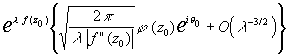 ,
где q0=(p
-y )/2, y=arg
f"(z0).
,
где q0=(p
-y )/2, y=arg
f"(z0).
Итак, окончательно при l>>1
и
f'(z0)=0
получим :
F(l )=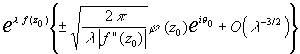 ,
где q0=(p
-y )/2, y=arg
f"(z0).
,
где q0=(p
-y )/2, y=arg
f"(z0).
Знак 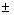 определяется направлением интегрирования.
определяется направлением интегрирования.
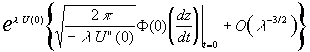 ;
U(0)=u(x0,y0); F (0)=j
(z0);
;
U(0)=u(x0,y0); F (0)=j
(z0);
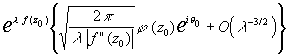 ,
где q0=(p
-y )/2, y=arg
f"(z0).
,
где q0=(p
-y )/2, y=arg
f"(z0).
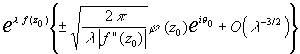 ,
где q0=(p
-y )/2, y=arg
f"(z0).
,
где q0=(p
-y )/2, y=arg
f"(z0).