- бесконечно удаленной точки.
- бесконечно удаленной точки.
I. Действия с комплексными числами.
1) Равенство.
Два комплексных числа равны, если равны их действительные и мнимые части:
z1=(a1,b1),
z2=(a2,b2). Если 1=z2
Ы a1=a2,
b1=b2. Операция сравнения не определена. Множество
комплексных чисел - неупорядоченное множество.
2) Сложение.
z1+z2=(a1+a2,b1+b2).
Пример:
(0,1)+(1,0)=(1,1).
3) Умножение. z1·z2=(a1 a2 -
b1b2,
a1b2+a2b1).
Операции сложения и
умножения включают действия с действительными числами.
Пример:
Умножение чисто вещественного числа на чисто мнимое число. (b,0)·(0,1)=(0,b)= ib - тем самым чисто мнимое
число есть произведение соответствующего действительного числа на мнимую
единицу.
Ю алгебраическая форма записи
комплексного числа z = a + ib = Re(z) + i·Im(z).
Обратные
операции.
4) Вычитание. z1 - z2 =
(a1 - a2, b1 - b2).
5)
Деление. 
.
Пример. 1/i = -i.
6) Возведение в целую степень. Действия с
многочленами.
Примеры: a) i2 = i i= (0,1)(0,1) = -1.
б) 
в) z= (a, b) =
a + ib. z2 = (a+ib)2 = a2 + 2iab -
b2 = (a2 - b2) + i 2ab Ю ; Re(z2)=(a2- b2),
Im(z2) = 2ab.
7) Комплексное сопряжение. z=(a, b)=a +
ib; Re(z) = a, Im(z) = b;
z* = (a, -b) = a - ib. Re(z*)
= a ; Im(z*) = -b. Ю; Re(z) = ( z +
z* ) / 2; Im(z) = (z - z* ) / 2i.
Некоторые
свойства. (z1 ±
z2)*= z1* ± z2* ; (z1
z2)* = z1*
z2*; (z1 / z2)* =
z1* / z2*;
(z*)* = z.
Примеры. а) z z* = (a +
ib)(a - ib) = a2 + b2; б) (z z) * =
(z2)* = (a2 - b2) - i 2ab; в)
z1 / z2 = z1 z2* /
z2 z2*; г) i* = -i; 1* =
1.
II. Геометрическая интерпретация комплексных
чисел.
z = (x, y) = x + iy Ы точка
плоскости (x, y).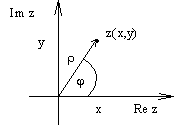
Взаимно однозначное соответствие.
Комплексная плоскость:
Ось абсцисс Re(z) - действительная ось
Ось ординат Im(z) -
мнимая ось
Простейшие множества точек на комплексной плоскости.
Примеры. а) |z-z0|=a (a>0) - окружность с центром в
точке z0 радиуса a;
б) |z-z0|<a (a>0) - открытый
круг с центром в точке z0 радиуса a;
в) |z-z0|>a
(a>0) - внешность открытого круг с центром в точке z0 радиуса a;
г) a<|z-z0 |<b (0<a<b) - открытое кольцо с центром в
точке z0 ;
д) arg(z-z0)= j -
луч, с началом в точке z0 , идущий под углом j к положительному направлению действительной оси.
е)
a <arg(z-z0)<b - внутренность неограниченного открытого сектора с вершиной
в точке z0 и углом раскрыва b -a .
ж) Re z= a - прямая, || мнимой оси, проходящая через
точку (a,0);
з) Im z= b - прямая, || действительной оси, проходящая через
точку (0,b);
Тригонометрическая и показательная формы записи комплексного числа
Полярные координаты (x,y) <=> (r ,j ), где x=.r cos
face=Symbol>j , y=r sin j ,
r
=(x2+y2)1/2=п zп =((Re z)2+(Im z)2)1/2 -
модуль комплексного числа,
tg j =y/x. j =j0+2p k- аргумент комплексного числа.
Arg z=arg z+2p k, 0
arg
z 2p .
Для комплексного числа 0=(0,0) модуль равен 0, а аргумент не определен.
Тригонометрическая форма записи комплексного числа: z=r (cosj +isinj )=r eij- (формула Эйлера)- показательная форма
записи комплексного числа.
Примеры. а)|z|2=z
z*=a2+b2.; z2 
|z|2;
б)z=1: |1|=1,
arg 1=0; 1=1(cos 0 +i sin 0)= 1ei0;
в) z=i: |i|=1, arg i=p /2; i=1(cos p /2 +i sin p /2)= 1eip /2;
г)
z=-1: |-1|=1, arg (-1)= p ; -1=1(cos p +i sin p )= 1eip ;
д) z=-i: |-i|=1, arg (-i)= 3p /2; -i=1(cos 3p /2 +i sin 3p /2)= 1ei3p /2;
e)
z=1+i: |1+i|=
, arg (1+i)= p /4; 1+i= (cos
p /4 +i sin p /4)= eip
/4;
ж) z=eij; |eij |=1, arg (eij)=
j ; eij=1 (cos
j +i sin j );
з)
z=-eij; |-eij
|=1, arg (-eij)= p +j ; -eij=1 (cos(p +j ) +i sin(p +j ))=ei(p +j )
Геометрическая интерпретация сложения и умножения. Теорема 1.1. "Необходимым и достаточным
условием сходимости Определение. Последовательность {zn} называется
ограниченной, Теорема 1.2. Из всякой ограниченной последовательности можно выделить
сходящуюся подпоследовательность. Критерий Коши. "Необходимым и достаточным условием сходимости
{zn} Неограниченно возрастающие последовательности .Если для " A>0 $ N(A):
Сложение двух
комплексных чисел можно рассматривать как сложение двух векторов на плоскости.
При этом справедливы
Неравенства треугольника
пz1+z2ппz1п+пz2п; пz1-z2п
пz1п-пz2п
пz1-z2п -
расстояние между z1 и z2 на комплексной плоскости.
e -окрестность точки z0: пz-z0п<e, 0<пz-z0п<e - выколотая (проколотая)
e -окрестность точки z0.
При
умножении двух комплексных чисел их модули перемножаются
(растяжение или сжатие), а аргументы складываются (поворот на
плоскости). z1=a1+i b1=r 1eia;
z2=a2+i b2=r2eib;
z1 z2=r1r2ei(a +b ) =>
|z1z2|=|z1||z2|;
arg(z1 z2)=arg z1+ arg z2 .
При делении двух комплексных чисел их модули делятся
(модуль знаменателя ╧ 0), а аргументы
вычитаются: z1/z2=(r1/r2)ei(a -b ) =>
z1/z2|=|z1|/|z2|;
arg(z1/z2)=arg z1- arg z2 .
Алгебраической формой записи комплексных чисел удобно пользоваться при
операциях сложения и вычитания, а показательной- при умножении, делении,
возведении в целую степень, извлечении целого корня (возведение в рациональную
степень).
Возведение в целую степень. zn=[r (cosj +isinj )]n=[r eij ]=rneinj=
=r
n(cos(nj )+isin(nj
)); Формула Муавра: (cosj
+isinj )n = cos(nj
)+isin(nj ).
Пример: (1+i)3=(eip
/4)3=23/2 ei3p
/4=23/2(cos(3p /4)+i sin(3p /4))=-2+2i ;
Извлечение целого корня (возведение в
рациональную степень).
z=r eij= r ei(j +2p k) , k=0,
1, 2...
. 
=>
корень n-той степени из комплексного числа имеет n различных значений, котторые
получаются при k=0, 1, 2...n-1.
Пример: 
=1 ei(0+2p k)/4={1 (k=0), i (k=1), -1 (k=2), -i (k=3) }.
2. Последовательности комплексных
чисел.
Определение
" Последовательностью комплексных чисел называют упорядоченное
счетное множество комплексных чисел."
Члены последовательности
(элементы) располагаются в порядке следования их номеров. Обозначение:
{zn}.
Сходящиеся последовательности.
Определение. "Комплексное число z называется пределом
последовательности {zn }, если для " e >0 $ N(e ): п
zn-zп <e для
" n N."
Обозначения: {zn}
z; 
zn=z.
Примеры. а) (1+z/n)n=ez, (z=x+iy); б) arg[(-1)n/n] не $ , т.к
arg[(-1)n/n]=0 при четных n, а при нечетных n
arg[(-1)n/n]=p .
Каждый член
последовательности zn=an+ibn :
{zn}={an}+i{bn}- одновременное задание двух
действительных последовательностей.
{zn} z= a+ib является требование {an} a; {bn} b."
Доказательство.
Необходимость. "e>0 $ N(e ): пzn-zп<e для " n N Юпan-aппzn-zп<e ,
пbn-bппzn-zп <e Ю {an} a, {bn} b.
Достаточность. "e >0 $ N1(e ): пan-aп <e /2 для " n N1, $ N2(e): пbn-bп<e /2 для " nN2ЮN=max{N1,N2}: пzn-zппan-aп+пbn-bп<e для " n N. n
если $ A: " n пznп<A.
Любая сходящаяся последовательность ограничена.
Доказательство. Основано на Теореме 1 и соответствующем свойстве сходящихся
ограниченных последовательностей вещественных чисел (Теорема Больцано-Вейерштрасса . Поскольку
{zn }ограничена, то соответствующие ей действительные
последовательности {an} и {bn} также ограничены
(пanп,пbnппan+i bnп
=(an2+bn2)1/2=пznп <A для " n).
Т.к. пanп<A Ю$ {ank} a: пaп <A. Последовательности {ank } соответствует
{bnk}: пbnkп<AЮ$ {bnl} b, причем
{anl} a
Ю (по Теореме 1
{znl}
z=a+ib: пzп<A. n
z
является требование, чтобы для " e >0 $ N(e ): пzn+m-znп<e для " n N и " m>0.
Доказательство. Основано на Теореме 1 и критерии Коши для последовательности
действительных чисел.
Необходимость. Т.к. последовательность
{zn} (zn= an+i bn ) сходится, то
сходятся и действительные последовательности. Ю для
" face=Symbol>e >0 и " m>0 $ N1(e):
пan+m-anп<e /2 для и $ N2(e): для " n N2(e).Ю$
N(e)= max{N1,N2}: пzn+m-znп<e для " n>N(e ) (в силу неравенства треугольника .
Достаточность.
Из того, что пzn+m-znп<e для Ю пan+m-anп,
пbn+m-bnппzn+m-znп<e , что является достаточными
условиями сходимости {an } и {bn}, т.е
{zn}-сходится. n
пznп >A для "T n>N(A), то
последовательность {zn} называется неограниченно
возрастающей.
Примеры. а) zn=zn при
|z|>1; б) zn= i n.
В обычном смысле они не сходятся, но
оказывается удобным считать, что
$ z =; zn= . Единственная бесконечно удаленная точка комплексной плоскости.
Все неограниченно возрастающие последовательности сходятся к этой
единственной точке. Если {zn} неограниченно возрастающая, то
{xn=1/zn} 0. Отсюда легко получить правила
арифметических действий с бесконечно удаленной точкой: 1/ =0,. 1/0= , z· = , z
0, z+ = , z/ =0,
z . Операции 0/0 и / являются неопределенными .
| Вверх | Вперед |
