Лекция 13.
Линейность
изображений.
Примеры 1) Полином.
2) sin
w t=(1/2i)(eiw
t-e-iw t) (1/2i)[1/(p-iw
)-1/(p+iw )]= w /(p2+w2);
(1/2i)[1/(p-iw
)-1/(p+iw )]= w /(p2+w2);
5. Теорема запаздывания.
f(t) A(a); f(t)
A(a); f(t) F(p);
ft (t)={0, t<t
; f(t-t ) t>t ;ft
(t)
F(p);
ft (t)={0, t<t
; f(t-t ) t>t ;ft
(t) A(a); ft
(t)
A(a); ft
(t)
 e-ptf(t-t
)dt=
e-ptf(t-t
)dt=
={t-t =t'}=e-pt e-pt'f(t')dt'=e-ptF(p).
e-pt'f(t')dt'=e-ptF(p).
Пример. Изображение прямоугольного
импульса.
f(t)={0, t<t1
; 1, t2<t<t1;
0, t>t2;} F(p)=(1/p)( e-pt
1- e-pt 2);
Пилообразный импульс- самостоятельно.
6. Изображение производной.
Пусть f(t) C[0;
C[0; ]
и имеет конечную производную f'(t), причем и f(t) и f'(t)
]
и имеет конечную производную f'(t), причем и f(t) и f'(t) A(a).
Пусть f(t)
A(a).
Пусть f(t) F(p). Найдем
f'(t)
F(p). Найдем
f'(t) ?.
?.
f'(t)
 e-ptf'(t)dt=(по
частям)=-f(0)+p
e-ptf'(t)dt=(по
частям)=-f(0)+p e-ptf(t)dt=(Rep>a)=pF(p)-f(0)=p[F(p)-f(0)/p];
e-ptf(t)dt=(Rep>a)=pF(p)-f(0)=p[F(p)-f(0)/p];
Аналогично, если f(t) C(n-1)[0;
C(n-1)[0; ]
и f(n)(t)- кусочно- непрерывна,
и f(k)(t)
]
и f(n)(t)- кусочно- непрерывна,
и f(k)(t) A(a),
k=0,1...n; то f(n)(t)
A(a),
k=0,1...n; то f(n)(t) pn[F(p)-f(0)/p-f'(0)/p2-...-f(n-1)(0)/pn];
pn[F(p)-f(0)/p-f'(0)/p2-...-f(n-1)(0)/pn];
7. Изображение интеграла.
f(t) A(a); j
(t)=
A(a); j
(t)=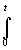 f(t
)dt О A(a); j
(t)
f(t
)dt О A(a); j
(t)
 e-pt
e-pt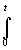 f(t
)dt dt=(Rep>a)=
f(t
)dt dt=(Rep>a)=
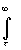 e-pt
f(t ) dtdt= =(1/p)
e-pt
f(t ) dtdt= =(1/p) e-ptf(t
)dt =(1/p)F(p);
e-ptf(t
)dt =(1/p)F(p);
Можно обобщить на случай n- кратного интеграла  (1/pn)F(p)
(1/pn)F(p)
8. Изображение свертки.
f1(t) A(a1),
f2(t)
A(a1),
f2(t) A(a2),
j
(t)=
A(a2),
j
(t)=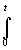 f1(t
)f2(t-t )dt
=
f1(t
)f2(t-t )dt
=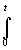 f1(t-t
)f2(t )dt
f1(t-t
)f2(t )dt A(a),
a=max(a1,a2);
A(a),
a=max(a1,a2);
j (t)
 e-pt
e-pt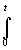 f1(t
)f2(t-t )dt
dt=(Rep>a)=
f1(t
)f2(t-t )dt
dt=(Rep>a)= f1(t
)
f1(t
)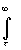 e-ptf2(t-t
)dt dt=(t-t =t')
=
e-ptf2(t-t
)dt dt=(t-t =t')
=
= f1(t
)e-pt
f1(t
)e-pt e-pt'f2(t')dt
dt'=F1(p)F2(p).
e-pt'f2(t')dt
dt'=F1(p)F2(p).
п.3. Решение
задачи Коши для линейного обыкновенного дифференциального уравнения с постоянными
коэффициентами операционным методом.
{a0y(n)(t)+...+any(t)=f(t), t>0; y(0)=...=y(n-1)(0)=0;
f(t) F(p); y(t)
F(p); y(t) Y(p);
=>
Y(p);
=>
=> Pn(p)Y(p)=F(p) => Y(p)=F(p)/Pn(p).
Надо найти оригинал по изображению. В нашем случае можно поступить проще.
Рассмотрим следующую задачу:
{a0g(n)(t)+...+ang(t)=0, t>0; g(0)=...=g(n-2)(0)=0;
g(n-1)(0)=1; g(t) G(p);
G(p);
Допустим, мы знаем ее решение. g(k)(t) pkG(p),
k=0,1,...n-1.; g(n)(t)
pkG(p),
k=0,1,...n-1.; g(n)(t) pn[G(p)-g(n-1)(0)/pn]=pnG(p)-1;
=> Pn(p)G(p)= a0 => G(p)= a0/Pn(p);
Y(p)=F(p)/Pn(p)= (1/a0) G(p) F(p); => y(t)
pn[G(p)-g(n-1)(0)/pn]=pnG(p)-1;
=> Pn(p)G(p)= a0 => G(p)= a0/Pn(p);
Y(p)=F(p)/Pn(p)= (1/a0) G(p) F(p); => y(t) (1/a0)G(p)F(p)=>y(t)=(1/a0)
(1/a0)G(p)F(p)=>y(t)=(1/a0)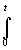 g(t-t
)f(t )dt
- Интеграл Дюгамеля.
g(t-t
)f(t )dt
- Интеграл Дюгамеля.
п.4. Теорема
Меллина.
Пусть F(p) C
C (Re p>a) и
(Re p>a) и
1) |F(p)|=>0 при |p|
 , Re p>a относительно аргумента.
, Re p>a относительно аргумента.
2) " x>a: 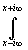 |F(p)|dy<M
(равномерно ограничен по x).
|F(p)|dy<M
(равномерно ограничен по x).
Тогда $
f(t) A(a): f(t)
A(a): f(t) F(p)
и f(t)=(1/2p i)
F(p)
и f(t)=(1/2p i)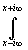 eptF(p)dp,
для " x>a.
eptF(p)dp,
для " x>a.
Замечание. Несобственный
интеграл (1/2p i)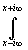 eptF(p)dp
вычисляется вдоль прямой
eptF(p)dp
вычисляется вдоль прямой
Re p=x>a и понимается в смысле главного
значения: 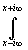 eptF(p)dp=
eptF(p)dp=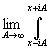 eptF(p)dp.
eptF(p)dp.
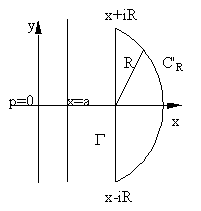
Доказательство. Рассмотрим
I(x,t)=(1/2p i)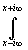 eptF(p)dp
(p=x+iy) и докажем:
eptF(p)dp
(p=x+iy) и докажем:
1. I(x,t) $
для " x>a;
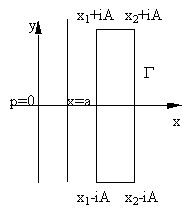 |
|I(x,t)| (1/2p )ext
(1/2p )ext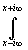 |F(p)|dy |F(p)|dy M'
ext=>I(x,t) $
для " x>a; M'
ext=>I(x,t) $
для " x>a;
Замечание: на "[0,T]
интеграл сходится равномерно по t.
2. Доказательство.
Т.к. F(p) C C (Re
p>a), то по теореме Коши *) (Re
p>a), то по теореме Коши *)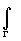 eptF(p)dp=0; Устремим
eptF(p)dp=0; Устремим
А  ,
тогда по условию 1. теоремы (|F(p)|=>0 при |p| ,
тогда по условию 1. теоремы (|F(p)|=>0 при |p|  , Re p>a) интегралы по горизонтальным отрезкам дадут в пределе 0.
, Re p>a) интегралы по горизонтальным отрезкам дадут в пределе 0. |
Интегралы по вертикальным прямым перейдут
в в несобственные интегралы => =>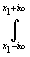 eptF(p)dp=
eptF(p)dp=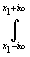 eptF(p)dp,
что в силу произвольности x1
и x2 доказывает утверждение.
eptF(p)dp,
что в силу произвольности x1
и x2 доказывает утверждение.
 |
3. Докажем,
что I(x,t)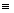 0, t<0. 0, t<0.
Рассмотрим I(x,t) при t<0. По теореме
Коши
*)
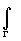 eptF(p)dp=0.
В силу замечания 2. к Лемме Жордана *)
при R eptF(p)dp=0.
В силу замечания 2. к Лемме Жордана *)
при R  интеграл по дуге С'R
интеграл по дуге С'R 0
при t<0. Поэтому f(t)=(1/2p i) 0
при t<0. Поэтому f(t)=(1/2p i)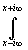 eptF(p)dp eptF(p)dp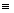 0, при t<0, Re p>a и " x>a.
0, при t<0, Re p>a и " x>a.
Итак, $
f(t)=(1/2p i)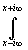 eptF(p)dp,
для " x>a. eptF(p)dp,
для " x>a. |
Из оценки интеграла => |f(t)|<Mext,
и inf(x)=a =>f(t) A(a).
A(a).
4. Покажем, что f(t) F(p).
F(p).
f(t)
 e-pt(1/2p
i)
e-pt(1/2p
i)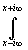 eqtF(q)dqdt={a<Req=x<Rep}=
(1/2p i)
eqtF(q)dqdt={a<Req=x<Rep}=
(1/2p i)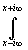 F(q)
F(q) e-(p-q)tdqdt=
=(1/2p i)
e-(p-q)tdqdt=
=(1/2p i)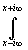 F(q)/(p-q)dq=(интеграл
можно вычислить с помощью вычетов, учитывая, что контур обходится по
часовой стрелке)=-Выч[F(q)/(p-q),q=p]=F(p)n
F(q)/(p-q)dq=(интеграл
можно вычислить с помощью вычетов, учитывая, что контур обходится по
часовой стрелке)=-Выч[F(q)/(p-q),q=p]=F(p)n
Замечание. Если $
аналитическое продолжение F(p) в левую полуплоскость, имеющее конечное
число N изолированных особых точек pn
и удовлетворяющее условиям Леммы Жордана *),
то f(t)=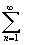 Выч[eptF(p),pn],
t
Выч[eptF(p),pn],
t 0.
0.
В частности, если F(p)=1/Pn(p),
где все нули полинома Pn(p)
лежат в левой полуплоскости Re p <a, то вычисление f(t) не представляет
трудностей.
Пример. Решить задачу
Коши: y"+w02y=f(t);
y(0)=y'(0)=0;
Y(p)=F(p)/(p2+w 02);
и трудности могут возникнуть при достаточно сложной F(p).
Но мы знаем, что y(t)=(1/a0)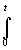 g(t-t
)f(t )dt *).
А т.к. G(p)= a0/Pn(p), и a0=1, и
Pn(p)=p2+w02
,
то G(p)=1/(p2+w02).
=> g(t)=(1/2p i)
g(t-t
)f(t )dt *).
А т.к. G(p)= a0/Pn(p), и a0=1, и
Pn(p)=p2+w02
,
то G(p)=1/(p2+w02).
=> g(t)=(1/2p i)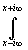 ept/(p2+w02)dp=
ept/(p2+w02)dp=
=Выч[ept/(p2+w02),
iw 0]+
Выч[ept/(p2+w 02),-iw0]=
eiw 0t/(2iw0)-e-iw
0t/(2iw0)=sin(w0t)/w0=>
y(t)=(1/w0)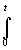 sin(w0(t-t
))f(t )dt
и в частности при f(t)= sin(w 0t):
y(t)=
sin(w0(t-t
))f(t )dt
и в частности при f(t)= sin(w 0t):
y(t)=
=(1/w0)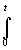 sinw0(t-t
)sin(w0t )dt
=(1/2w 02)[sin(w0t)-tw0cos(w0t)]-
осциллирующая функция с линейно нарастающей амплитудой- резонанс.
sinw0(t-t
)sin(w0t )dt
=(1/2w 02)[sin(w0t)-tw0cos(w0t)]-
осциллирующая функция с линейно нарастающей амплитудой- резонанс.
п.5. Изображение
произведения.
Пусть f1(t) A(a1):
f1(t)
A(a1):
f1(t) F1(p)
F1(p) C
C (Re
p>a1); f2(t)
(Re
p>a1); f2(t) A(a2):
f2(t)
A(a2):
f2(t) F2(p)
F2(p) C
C (Re
p>a2).
(Re
p>a2).
f(t)=f1(t)f2(t) A(a1+a2);
-удовлетворяет всем условиям существования изображения.
A(a1+a2);
-удовлетворяет всем условиям существования изображения.
f(t) F(p)=
F(p)= e-ptf1(t)f2(t)dt={f1(t)=(1/2p
i)
e-ptf1(t)f2(t)dt={f1(t)=(1/2p
i)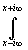 eptF1(p)dp,
для " x>a1}=
eptF1(p)dp,
для " x>a1}=
=(1/2p i) e-ptf2(t)
e-ptf2(t)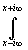 eqtF1(q)dqdt=(1/2p
i)
eqtF1(q)dqdt=(1/2p
i)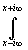 F1(q)
F1(q) e-(p-q)tf2(t)dtdq=
e-(p-q)tf2(t)dtdq=
=(1/2p i)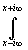 F1(q)F2(p-q)dq;
(a1<x=Re q<Re p- a2)=(1/2p
i)
F1(q)F2(p-q)dq;
(a1<x=Re q<Re p- a2)=(1/2p
i)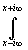 F1(p-q)F2(q)dq;
F1(p-q)F2(q)dq;
(a2<x=Re q<Re p- a1) ; F(p) C
C (Re
p>a1+a2)
(Re
p>a1+a2)
Пример. f1(t)=t 1/p2;
f2(t)=sinw t
1/p2;
f2(t)=sinw t w
/(p2+w 2);
w
/(p2+w 2);
f(t)=f1(t)f2(t)=tsinw
t (w
/2p i)
(w
/2p i)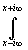 dq/[(p-q)2(q2+w2)]
; 0<x=Re q<Re p={при помощи вычетов,
с учетом того, что контур интегрирования замыкается вправо и обходится
по
часовой стрелке- в отрицательном направлении}= -w
Выч[1/[(p-q)2(q2+w2)],q=p]
dq/[(p-q)2(q2+w2)]
; 0<x=Re q<Re p={при помощи вычетов,
с учетом того, что контур интегрирования замыкается вправо и обходится
по
часовой стрелке- в отрицательном направлении}= -w
Выч[1/[(p-q)2(q2+w2)],q=p]
{q=p- полюс 2-го порядка
*}=-w
d/dq[1/(q2+w2),q=p] =2w
p/(p2+w2);
Замечание. Можно считать
контур интегрирования замкнутым налево и суммировать вычеты в 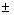 iw ;
iw ;
![]() G(p);
G(p);
![]() pkG(p),
k=0,1,...n-1.; g(n)(t)
pkG(p),
k=0,1,...n-1.; g(n)(t)![]() pn[G(p)-g(n-1)(0)/pn]=pnG(p)-1;
=> Pn(p)G(p)= a0 => G(p)= a0/Pn(p);
Y(p)=F(p)/Pn(p)= (1/a0) G(p) F(p); => y(t)
pn[G(p)-g(n-1)(0)/pn]=pnG(p)-1;
=> Pn(p)G(p)= a0 => G(p)= a0/Pn(p);
Y(p)=F(p)/Pn(p)= (1/a0) G(p) F(p); => y(t)![]() (1/a0)G(p)F(p)=>y(t)=(1/a0)
(1/a0)G(p)F(p)=>y(t)=(1/a0)![]() g(t-t
)f(t )dt
- Интеграл Дюгамеля.
g(t-t
)f(t )dt
- Интеграл Дюгамеля.
![]() C
C![]() (Re p>a) и
(Re p>a) и
![]()
![]() , Re p>a относительно аргумента.
, Re p>a относительно аргумента.
![]() |F(p)|dy<M
(равномерно ограничен по x).
|F(p)|dy<M
(равномерно ограничен по x).
![]() A(a): f(t)
A(a): f(t)![]() F(p)
и f(t)=(1/2p i)
F(p)
и f(t)=(1/2p i)![]() eptF(p)dp,
для " x>a.
eptF(p)dp,
для " x>a.
![]() eptF(p)dp
вычисляется вдоль прямой
eptF(p)dp
вычисляется вдоль прямой
![]() eptF(p)dp=
eptF(p)dp=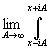 eptF(p)dp.
eptF(p)dp.
![]() eptF(p)dp
(p=x+iy) и докажем:
eptF(p)dp
(p=x+iy) и докажем:


![]() F(p)=
F(p)=![]() e-ptf1(t)f2(t)dt={f1(t)=(1/2p
i)
e-ptf1(t)f2(t)dt={f1(t)=(1/2p
i)![]() eptF1(p)dp,
для " x>a1}=
eptF1(p)dp,
для " x>a1}=
![]() e-ptf2(t)
e-ptf2(t)![]() eqtF1(q)dqdt=(1/2p
i)
eqtF1(q)dqdt=(1/2p
i)![]() F1(q)
F1(q)![]() e-(p-q)tf2(t)dtdq=
e-(p-q)tf2(t)dtdq=
![]() F1(q)F2(p-q)dq;
(a1<x=Re q<Re p- a2)=(1/2p
i)
F1(q)F2(p-q)dq;
(a1<x=Re q<Re p- a2)=(1/2p
i)![]() F1(p-q)F2(q)dq;
F1(p-q)F2(q)dq;
![]() C
C![]() (Re
p>a1+a2)
(Re
p>a1+a2)
![]() 1/p2;
f2(t)=sinw t
1/p2;
f2(t)=sinw t![]() w
/(p2+w 2);
w
/(p2+w 2);
![]() (w
/2p i)
(w
/2p i)![]() dq/[(p-q)2(q2+w2)]
; 0<x=Re q<Re p={при помощи вычетов,
с учетом того, что контур интегрирования замыкается вправо и обходится
по
часовой стрелке- в отрицательном направлении}= -w
Выч[1/[(p-q)2(q2+w2)],q=p]
dq/[(p-q)2(q2+w2)]
; 0<x=Re q<Re p={при помощи вычетов,
с учетом того, что контур интегрирования замыкается вправо и обходится
по
часовой стрелке- в отрицательном направлении}= -w
Выч[1/[(p-q)2(q2+w2)],q=p]
![]() iw ;
iw ;