Лекция 2.
- §4. Дифференцирование функции
комплексной переменной. Понятие аналитической функции комплексной
переменной.
- 1. Теорема 1) Условия
Коши-Римана.
Теорема 2) Достаточные условия дифференцируемости f(z) в
точке z0Оg
- 2. Определение f(z) аналитической в
области g.
Теорема 3) Необходимое и достаточное условие аналитичности
f(z) в g.
Замечание о возможности опустить условие f'(z)О C(g).
- 3. Свойства аналитической функции
комплексной переменной.
Дифференцирование функций комплексной переменной. Понятие
аналитической функции.
Пусть f(z) C(g).
C(g).
Определение. f(z) называется дифференцируемой (или
моногенной) в точке z0 g, если при Dz
g, если при Dz 0 (D z = z-z0) $конечный предел разностного отношения
0 (D z = z-z0) $конечный предел разностного отношения
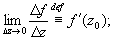 где z0
где z0 g.
g.
Центральная идея теории функций комплексной
переменной возникает при формулировке понятия производной. На первый взгляд эта
производная определяется совершено аналогично производной функции действительной
переменной, как предел разностного отношения 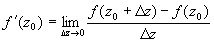 .
.
Однако, приращение комплексного аргумента D z характеризуется не только
величиной |D z|, но
и направлением arg D z, а производная по определению от этого направления не
зависит. Поэтому дифференцируемость функции комплексного переменного-
значительно более редкое явление, чем дифференцируемость функции вещественного
переменного, а дифференцируемые функции комплексного переменного- аналитические
функции- обладают гораздо более единообразными свойствами, чем дифференцируемые
функции действительной переменной.
Важнейшая задача ТФКП- обсудить свойство аналитичности с
разнообразных точек зрения, дать его характеристики на разных языках.
Теорема
4.1. Если f(z)=u(x,y)+iv(x,y)
дифференцируема(моногенна) в точке z0,
то $ux(x0,y0),
uy(x0,y0),
vx(x0,y0),
vy(x0,y0), причем
они связаны условиями
Коши-Римана:
ux(x0,y0)=vy(x0,y0)
;
uy(x0,y0)=-vx(x0,y0).
Доказательство.
D z=D x+iD y. Т.к. предел, если он
$ , не зависит от
способа стремления Dz 0, то положим
сначала Dz=Dx. Получим
0, то положим
сначала Dz=Dx. Получим
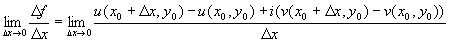
=
ux(x0,y0)+
ivx(x0,y0)=*. Положив Dz=iD y получим *=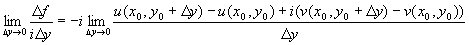
=
-iuy(x0,y0)+vy(x0,y0).
Приравнивая вещественную и мнимую часть получим
ux(x0,y0)=vy(x0,y0)
;
uy(x0,y0)=-vx(x0,y0). - условия Коши-Римана. n
Пусть f(z) C(g) и f(z)=u(x,y)+iv(x,y).
C(g) и f(z)=u(x,y)+iv(x,y).
Теорема 4.2Если в точке
z0=(x0,y0)  g $ первые дифференциалы функций u(x,y) и v(x,y) и первые
частные производные этих функций в точке (x0,y0)
связаны условиями Коши-Римана , то f(z) √ дифференцируемая (моногенная) функция в
точке z0.
g $ первые дифференциалы функций u(x,y) и v(x,y) и первые
частные производные этих функций в точке (x0,y0)
связаны условиями Коши-Римана , то f(z) √ дифференцируемая (моногенная) функция в
точке z0.
Доказательство. Заметим, что $ первых дифференциалов означает, что
D u= ux(x0,y0)D x+uy(x0,y0)D y+x (x,y);  Аналогично
Аналогично
D v= vx(x0,y0)D x+vy(x0,y0)D y+h (x,y); 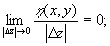 Обозначим V(x,y)=x (x,y)+ih (x,y).
Обозначим V(x,y)=x (x,y)+ih (x,y).
Тогда 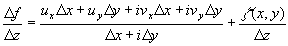 =(т.к.
uy=-vx и
vy=ux).
=(т.к.
uy=-vx и
vy=ux).
 ux(x0,y0)+ivx(x0,y0)+
ux(x0,y0)+ivx(x0,y0)+
=> $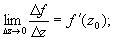 n
n
Замечания.
1) Эквивалентные
формы записи производной:
f▓(z)=ux(x,y)+ivx(x,y)=vy(x,y)+ivx(x,y)=ux(x,y)-iuy(x,y)=vy(x,y)-iuy(x,y)
2) Теорема
4.2 не является
обратной к >теореме 4.1.
3) Равенство 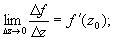 равносильно тому, что для "e>0 $d (e )>0: такое, что
равносильно тому, что для "e>0 $d (e )>0: такое, что
|Df/D z - f '(z0)|< e
как только |Dz|<d. => Если f(z) дифференцируема (моногенна) в точке z0, то она и непрерывна в этой точке. Обратное, вообще
говоря, неверно.
Основное
определение.Функция f(z) C(g), дифференцируемая (моногенная) во всех точках z
C(g), дифференцируемая (моногенная) во всех точках z g, производная которой f ' (z)
g, производная которой f ' (z) C(g) называется
аналитической функцией в области g.
C(g) называется
аналитической функцией в области g.
Обозначение: f(z) C
C (g).
(g).
Понятие
аналитичности функции определяет глобальное поведение f(z) в области g.
Теорема 4.3.Необходимым и достаточным условиями аналитичности функции
f(z)=u(x,y)+iv(x,y) в области g, являются непрерывность первых частных
производных ux, uy, vx,
vy и связь их условиями Коши-Римана .
Доказательство.
Необходимость. f(z) C
C (g) => f'(z)
(g) => f'(z) C(g) =>ux, uy,
vx, vy
C(g) =>ux, uy,
vx, vy C(g). Выполнение условий Коши-Римана следует из Теоремы 4.1 .
C(g). Выполнение условий Коши-Римана следует из Теоремы 4.1 .
Достаточность. ux, uy,
vx , vy C(g)=>
$первые дифференциалы
функций u(x,y), v(x,y) => по теореме 4.2 $ f
'(z)
C(g)=>
$первые дифференциалы
функций u(x,y), v(x,y) => по теореме 4.2 $ f
'(z) C(g)=ux+ivx;непрерывность
f'(z) следует из непрерывности
ux , vx.n
C(g)=ux+ivx;непрерывность
f'(z) следует из непрерывности
ux , vx.n
Замечание. В дальнейшем будет
показано, что из f(z) C
C (g) => f '(z)
(g) => f '(z) C
C (g) и для
"n $
f(n)(z)
(g) и для
"n $
f(n)(z) C
C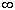 (g), что
оправдывает введенное определение.
(g), что
оправдывает введенное определение.
Основное замечание. Включение в основное определение условия f '(z) C(g) - масло масляное. Основное
определение может быть таким: "f(z)
называется "аналитической" в g,
если она дифференцируема(моногенна) во всех
точках z
C(g) - масло масляное. Основное
определение может быть таким: "f(z)
называется "аналитической" в g,
если она дифференцируема(моногенна) во всех
точках z g." и вместо Теоремы
4.2 будет
g." и вместо Теоремы
4.2 будет
Теорема 4.4.Если u(x,y)
и v(x,y)  C(g) и в точке
z0=(x0,y0)
C(g) и в точке
z0=(x0,y0) g $первые частные производные ux,
uy, vx , vy
связаные условиями Коши-Римана , то f(z) √ дифференцируемая (моногенная) функция в
точке z0.
g $первые частные производные ux,
uy, vx , vy
связаные условиями Коши-Римана , то f(z) √ дифференцируемая (моногенная) функция в
точке z0.
Доказательство
достаточно сложное (см. например И.И. Привалов "Введение в теорию функций
комплексной переменной.")
и вместо
Теоремы 4.3 будет
Теорема
4.5. Необходимым и достаточным условиями "аналитичности"
функции f(z)=u(x,y)+iv(x,y) в области g, являются непрерывность u(x,y),
v(x,y) и в " точке z=(x,y) g $ первые частные производные ux,
uy, vx, vy,
связанные условиями Коши-Римана"
.
g $ первые частные производные ux,
uy, vx, vy,
связанные условиями Коши-Римана"
.
Однако, оказывается, что f ' (z)
"аналитической функции" непрерывна в g, причем для "n f(n)(z) C(g), т.е. класс "аналитических
функций" не является расширением введенного нами класса, а полностью с ним
совпадает!! Поэтому мы будем пользоваться введенным определением, что в
дальнейшем облегчит нам многие доказательства!!
C(g), т.е. класс "аналитических
функций" не является расширением введенного нами класса, а полностью с ним
совпадает!! Поэтому мы будем пользоваться введенным определением, что в
дальнейшем облегчит нам многие доказательства!!
Следствия условий Коши-Римана :
Попробуйте показать самостоятельно, что
1) Действительная и мнимая части аналитической
функции удовлетворяют уравнению Лапласа:
uxx+uyy=Du=0 ; vxx+vyy=Dv=02) Действительная и мнимая части
аналитической функции f(z)=u(r ,j )+iv(r ,j
) комплексной переменной z=r eijсвязаны соотношениями:
vj =r ur , uj =-r vr.3) Модуль и аргумент
аналитической функции f(z)=R(x,y)eiF
(x,y) связаны соотношениями:
Rx=RFy, Ry=-RFx
п.3. Свойства аналитических функций.
1) Если f(z) C
C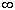 (g) (аналитическая в g), то f(z)
(g) (аналитическая в g), то f(z) C(g)
(непрерывна в g).
C(g)
(непрерывна в g).
2) Сумма и
произведение аналитических функций есть аналитическая функция. Частное
аналитических функций есть аналитическая функция всюду, где знаменатель отличен
от нуля.
3) Если w=f(z) C
C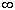 (g) -
аналитическая функция комплексной переменной z, причем в области ее значений G на плоскости w
определена аналитическая функция
(g) -
аналитическая функция комплексной переменной z, причем в области ее значений G на плоскости w
определена аналитическая функция
x=j (w) C
C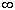 (G), то функция F(z)= j
[f(z)]
(G), то функция F(z)= j
[f(z)] C
C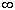 (g) -аналитическая функция комплексной переменной z
в области g.
(g) -аналитическая функция комплексной переменной z
в области g.
4) Пусть w=f(z)=u(x,y)+iv(x,y) C
C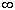 (g) и f
'(z0)
(g) и f
'(z0) 0, z0
0, z0 g. Тогда
в окрестности точки w0=f(z0) определена обратная аналитическая функция z=j (w)
g. Тогда
в окрестности точки w0=f(z0) определена обратная аналитическая функция z=j (w) C
C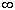 (|w-w0|<e ) отображающая эту окрестность на окрестность точки
z0, причем j '(w0)=1/ f '(z0).
(|w-w0|<e ) отображающая эту окрестность на окрестность точки
z0, причем j '(w0)=1/ f '(z0).
Доказательство. Для существования
обратной функции необходимо, чтобы уравнения u=u(x,y), v=v(x,y) можно было
разрешить относительно x, y в окрестности точки
w0. Т.е. эти уравнения задают
неявные функции x,y как функции u,v. Для этого достаточно, чтобы в окрестности
точки z0 выполнялось
условие: 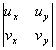
 0. Но
0. Но 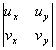 =uxvy-uyvx=( Коши-Риман =
ux2+vy2=|f '(z0)|
=uxvy-uyvx=( Коши-Риман =
ux2+vy2=|f '(z0)| 0. Доказано
существование обратной функции z=j(w). Cоставив разностное отношение
0. Доказано
существование обратной функции z=j(w). Cоставив разностное отношение  можно доказать существование и
непрерывность производной j'(w0) при условии |f '(z0)|
можно доказать существование и
непрерывность производной j'(w0) при условии |f '(z0)| 0.n
0.n
5) Пусть в односвязной
области g плоскости (x,y) задана функция u(x,y), являющаяся действительной частью аналитической функции
f(z). Тогда мнимая часть этой функции
определяется с точностью до аддитивной постоянной.
Доказательство. В силу условий Коши-Римана дифференциал неизвестной функции v(x,y) однозначно определен по функции u(x,y):
dv=vxdx+vydy=-uydx+uxdy. Функцию двух действительных переменных можно определить
по ее полному дифференциалу с точностью до аддитивной постоянной.n
6) grad
u=(ux,uy), grad v=(vx,vy), (grad u,
grad v)=uxvx+ uy vy=- uy
vy+ uy vy=0. Т.к. градиент ортогонален линии уровня => линии уровня
u(x,y)=c, v(x,y)=c взаимно ортогональны.
Примеры простейших функций комплексной
переменой.
1) Константа: f(z)=C -
аналитическая на расширенной комплексной
плоскости.
f '(z)=0.
2) Линейная функция f(z)=az+b аналитическая на всей комплексной плоскости.
f
'(z)=a.
3) f(z)=1/z - аналитическая всюду,
кроме точки z=0.
4) f(z)=zn n-целое число- аналитическая на всей комплексной плоскости.
f '(z)=nzn-1
5) f(z)= z* =x-iy - не аналитическая. ux=1 vy=-1;
vy=-1;
 ux(x0,y0)+ivx(x0,y0)+
ux(x0,y0)+ivx(x0,y0)+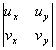
 можно доказать существование и
непрерывность производной j'(w0) при условии |f '(z0)|
можно доказать существование и
непрерывность производной j'(w0) при условии |f '(z0)|