Лекция 3.
- §5. Интеграл от функции комплексной
переменной по кривой на комплексной плоскости.
- 1. Вспомогательные положения.
Кусочно-гладкая кривая. Криволинейные интегралы II рода.
- 2. Определение интеграла от функции
комплексной переменной.
- 3. Свойства
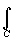 f(z)dz.
f(z)dz.
Вспомогательные
положения.
1) Кусочно-гладкая кривая- Множество точек z=z(t)=x(t)+iy(t), где t [a,b] действительный параметр. x(t), y(t)
[a,b] действительный параметр. x(t), y(t)  C[a,b]; x'(t), y'(t) -кусочно- непрерывные на [a,b];.
x'2(t)+y'2(t)
C[a,b]; x'(t), y'(t) -кусочно- непрерывные на [a,b];.
x'2(t)+y'2(t)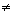 0 - нет точек
возврата, нет точек самопересечения. Если замкнутая кривая, то x(a)=x(b),
y(a)=y(b).
0 - нет точек
возврата, нет точек самопересечения. Если замкнутая кривая, то x(a)=x(b),
y(a)=y(b).
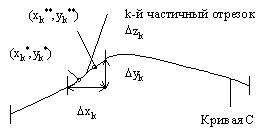
2) Криволинейные интегралы второго рода по кривой на
плоскости (x,y).
 P(x,y)dx+Q(x,y)dy=
P(x,y)dx+Q(x,y)dy=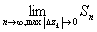 ; ;
Sn=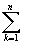 P(xk*,yk*)D
xk+Q(xk**,yk**)D yk; P(xk*,yk*)D
xk+Q(xk**,yk**)D yk;
|D
zk|=[(D
xk)2+(D
yk)2]1/2. При этом предел не зависит ни от способа
разбиения, ни от выбора промежуточных точек. |
 |
Достаточными
условиями существования криволинейного интеграла II рода являются : кусочная
гладкость кривой C, кусочная непрерывность и ограниченность функций P и
Q.
Основное определение.
Интегралом от функции комплексно
переменной f(z)=u(x,y)+iv(x,y) по кривой C комплексной плоскости z
называется комплексное число, действительная и мнимая части которого есть
криволинейные интегралы второго рода от действительной и мнимой частей f(z)
вида:
 f(z)dz =
f(z)dz = [u(x,y)+iv(x,y)]
(dx+idy)=
[u(x,y)+iv(x,y)]
(dx+idy)= udx-vdy +i
udx-vdy +i vdx+udy.
vdx+udy.
Замечания.
1)
Достаточное условие существования- кусочная гладкость контура C и кусочная
непрерывность и ограниченность |f(z)|.
2) Из этого определения и
определения криволинейного интеграла II рода
=> $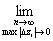 Sn=
Sn= f(z)dz; Sn=
f(z)dz; Sn=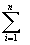 f(zi*)D zi, причем предел
не зависит ни от способа разбиения, ни от выбора промежуточных точек.
f(zi*)D zi, причем предел
не зависит ни от способа разбиения, ни от выбора промежуточных точек.
Свойства f(z)dz .
f(z)dz .
Поскольку значение контурного интеграла зависит от
направления интегрирования, условимся в качестве положительного направления обхода
контура принимать направление, при котором внутренняя область, ограниченная
данным замкнутым контуром, остается слева от
направления движения. Интегрирование в положительном направлении будем
обозначать символом тc+ f(z)dz или просто тc
f(z)dz, интегрирование в отрицательном
направлении- 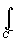 f(z)dz.
f(z)dz.
1) 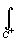 f(z)dz=-
f(z)dz=-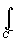 f(z)dz;
2) Линейность. 3)
f(z)dz;
2) Линейность. 3) 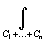 f(z)dz=
f(z)dz=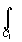 f(z)dz+┘+
f(z)dz+┘+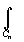 f(z)dz.
f(z)dz.
4) | f(z)dz|
f(z)dz|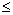
 |f(z)|ds
|f(z)|ds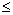 MLc;
MLc;
5) Вычисление
интеграла интегрированием по параметру:  f(z)dz=
f(z)dz=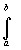 f[z(t)] z '(t)dt.
f[z(t)] z '(t)dt.
Пример. 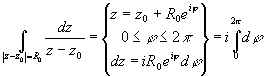 =2p i . Результат не зависит
ни от R0, ни от
z0 !!
=2p i . Результат не зависит
ни от R0, ни от
z0 !!
6) Замена переменных. Пусть $ j (x ): z=j (x ); C<=> G на плоскости x и j (x )О
C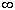 (D) и однолистная в D, где D- область комплексной
плоскости x ,
содержащая G .
(D) и однолистная в D, где D- область комплексной
плоскости x ,
содержащая G .
=> f(z)dz=
f(z)dz=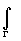 f[j (x )]j '(x
)dx .
f[j (x )]j '(x
)dx .

![]() f(z)dz .
f(z)dz . ![]() f(z)dz.
f(z)dz. ![]() f(z)dz=-
f(z)dz=-![]() f(z)dz;
2) Линейность. 3)
f(z)dz;
2) Линейность. 3) ![]() f(z)dz=
f(z)dz=![]() f(z)dz+┘+
f(z)dz+┘+![]() f(z)dz.
f(z)dz. ![]() f(z)dz|
f(z)dz|![]()
![]() |f(z)|ds
|f(z)|ds![]() MLc;
MLc; ![]() f(z)dz=
f(z)dz=![]() f[z(t)] z '(t)dt.
f[z(t)] z '(t)dt. 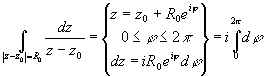 =2p i . Результат не зависит
ни от R0, ни от
z0 !!
=2p i . Результат не зависит
ни от R0, ни от
z0 !!
![]() (D) и однолистная в D, где D- область комплексной
плоскости x ,
содержащая G .
(D) и однолистная в D, где D- область комплексной
плоскости x ,
содержащая G . ![]() f(z)dz=
f(z)dz=![]() f[j (x )]j '(x
)dx .
f[j (x )]j '(x
)dx .