Лекция 3.
- § 6. Теорема Коши.
- 1. Вспомогательные положения.
Квадрируемая область. Формула Грина.
- 2. Теорема Коши. Случай многосвязной
области.
- 3. Неопределенный интеграл функции
комплексной переменной. Свойства неопределенного интеграла функции
комплексной переменной. Формула Коши-Адамара.
1. Вспомогательные положения. Квадрируемая область.
Формула Грина.
1)
Определение. Область g плоскости (x,y) называется квадрируемой еслиsup множества площадей всех вписанных
многоугольников P* равна
inf множества площадей всех
описанных многоугольников P*. Число P=P*=P* называют площадью плоской области g (по
Жордану). Достаточное условие квадрируемости- кусочная гладкость (спрямляемость)
границы - 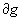 .
.
2) Для функции f(x,y) C(g) и |f(x,y)|
C(g) и |f(x,y)|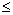 A- кусочно непрерывной и ограниченной в
квадрируемой области g $
A- кусочно непрерывной и ограниченной в
квадрируемой области g $ 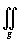 f(x,y)dxdy, понимаемый как предел последовательности
соответствующих интегральных сумм.
f(x,y)dxdy, понимаемый как предел последовательности
соответствующих интегральных сумм.
3)
Определение .Область g на плоскости называется
односвязной, если для " замкнутого контура 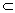 g, ограниченная им часть плоскости
целиком
g, ограниченная им часть плоскости
целиком 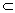 g.
g.
4) Формула Грина. Пусть P(x,y), Q(x,y)  C(
C(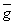 ),
причем
),
причем 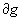 - кусочно-
гладкий контур и Px, Py, Qx,
Qy
- кусочно-
гладкий контур и Px, Py, Qx,
Qy  C(g), тогда
C(g), тогда
 Pdx+Qdy=
Pdx+Qdy=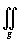 (Qx - Py) dxdy.
(Qx - Py) dxdy.
2. Теорема Коши. Случай многосвязной
области.
Теорема Коши. Если f(z) C
C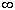 (g), в односвязной области g, то для "замкнутого
контура g
(g), в односвязной области g, то для "замкнутого
контура g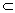 g
g 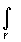 f(z)dz =0.
f(z)dz =0.
Доказательство.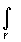 f(z)dz=
f(z)dz=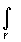 udx-vdy+i
udx-vdy+i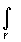 vdx+udy= (по формуле Грина)
vdx+udy= (по формуле Грина)
=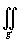 (-vx-uy)dxdy+i
(-vx-uy)dxdy+i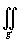 (ux-vy)dxdy= (из условия Коши-Римана : ux=vy;
uy=-vx
(ux-vy)dxdy= (из условия Коши-Римана : ux=vy;
uy=-vx
=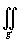 (uy-uy)dxdy+i
(uy-uy)dxdy+i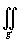 (vy-vy)dxdy=0. n
(vy-vy)dxdy=0. n
Замечания.
1) Требование односвязности
области является существенным. Например, пусть область g представляет собой
круговое кольцо 1<|z|<3. Функций f(z)=1/z C
C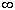 (g).
(g).
Однако,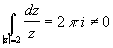 . Это связан в
частности с тем, что контур |z|=2 не образует полную границу области
аналитичности f(z).
. Это связан в
частности с тем, что контур |z|=2 не образует полную границу области
аналитичности f(z).
2)ОпределениеФункция называется аналитической в
замкнутой области g
( f(z) C
C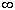 (
(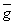 ) ), если f(z)
) ), если f(z) C
C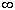 (g) и
f(z)
(g) и
f(z)  C (
C (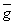 ). Т.е. f(z)
). Т.е. f(z) C(
C(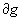 ). Определение
справедливо и для многосвязной области.
). Определение
справедливо и для многосвязной области.
II-я Теорема
Коши. Если f(z) C
C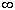 (
(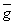 ), g-односвязная, то
), g-односвязная, то  f(z)dz =0.
f(z)dz =0.
Теорема переносится и на случай многосвязной
области.
Теорема Пусть f(z) C
C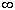 (g),
g-многосвязная, ограниченная извне контуром C0, а изнутри- контурами C1,
C2,...,Cn и пусть f(z)
(g),
g-многосвязная, ограниченная извне контуром C0, а изнутри- контурами C1,
C2,...,Cn и пусть f(z) C
C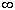 (
(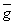 ). Тогда
). Тогда  f(z)dz =0,
где С-полная граница g, С= C0
f(z)dz =0,
где С-полная граница g, С= C0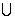 C1
C1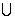 C2
C2 ...
... Cn, проходящая в положительном
направлении.
Cn, проходящая в положительном
направлении.
| Доказательство. Проведем
гладкие кривые g 1,g2,...,gn,
соединяющие контур C0 с контурами C1,
C2,...,Cn и не
пересекающиеся между собой . Тогда область, ограниченная кривыми
C0,C1,C2,...,Cn
и кривыми g1,g2,...,gn,
проходимыми дважды в противоположных направлениях оказывается
односвязной. По II
теореме Коши интеграл по
границе этой области равен 0. Но интегралы по |
 |
вспомогательным
кривым g1,g2,...,gn
проходятся дважды в противоположных
направлениях и при суммировании интегралов выпадают. Поэтому
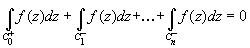 . n
. n
3. Неопределенный интеграл
функции комплексной переменной. Свойства неопределенного интеграла функции
комплексной переменной. Формула Коши-Адамара.
Следствия
теоремы Коши.
1) Если g- односвязная и f(z) C
C (g), то для
" z1,z2
(g), то для
" z1,z2 g
g 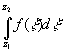 не зависит от
пути
не зависит от
пути
интегрирования. При фиксированном
z0 интеграл =F(z)- функция только z!
=F(z)- функция только z!
2) Неопределенный
интеграл. Пусть g-односвязная область, f(z) C(g), для " замкнутого контура
g
C(g), для " замкнутого контура
g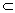 g интеграл
g интеграл 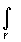 f(z)dz =0. Функция
f(z)dz =0. Функция  =F(z)- называется неопределенным интегралом от f(z).
=F(z)- называется неопределенным интегралом от f(z).
Каковы свойства F(z) ?
Теорема 6.1. Если
g-односвязная и f(z) C(g) и для " замкнутого контура
g
C(g) и для " замкнутого контура
g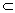 g интеграл
g интеграл 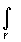 f(z)dz =0, то F(z)
$ и F(z)
f(z)dz =0, то F(z)
$ и F(z) C
C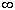 (g).
(g).
Доказательство. 
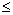
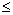
 <e при
п D zп <d =>$
<e при
п D zп <d =>$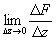 =F'(z)=f(z)
=F'(z)=f(z) C(g)
C(g)
=>F(z) C
C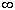 (g) n
(g) n
Свойства неопределенного интеграла.
1) Понятие
первообразной. Пусть f(z) C(g). Тогда первообразной F(z) функции
f(z) в g называется " F(z)
C(g). Тогда первообразной F(z) функции
f(z) в g называется " F(z) C
C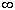 (g)
такая, что F '(z)=f(z).
(g)
такая, что F '(z)=f(z).
Замечания.
1)
Неопределенный интеграл F(z) в односвязной области g- первообразная f(z).
2) Если $ первообразная F(z), то их $ бесконечно много, но все они
различаются на аддитивную постоянную F'1(z)-
F'2(z)=0 => F1(z)=F2(z)+C.
3) Формула Ньютона-Лейбница. Если g-односвязная и и
f(z) C(g) и для
" замкнутого
контура g
C(g) и для
" замкнутого
контура g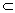 g интеграл
g интеграл 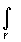 f(z)dz
=0, то
f(z)dz
=0, то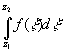 =F(z2)-F(z1);
где F- "
первообразная.
=F(z2)-F(z1);
где F- "
первообразная.
4) Формула конечных
приращений, вообще гооворя не верна.
f(b)-f(a)=(b-a)f'(x*); x* (a,b).
(a,b).
5) Формула Коши-Адамара.
Пусть g- односвязная и f(z) C
C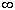 (g) и для " замкнутого контура g
(g) и для " замкнутого контура g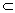 g
интеграл
g
интеграл 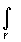 f'(x )dx =0; f(z)- первообразная f '(z) =>
f'(x )dx =0; f(z)- первообразная f '(z) =>
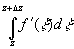 =f(z+D z)-f(z). В качестве пути
интегрирования возьмем прямолинейный отрезок, соединяющий z и z+D z: x =z+D
zq ; 0
=f(z+D z)-f(z). В качестве пути
интегрирования возьмем прямолинейный отрезок, соединяющий z и z+D z: x =z+D
zq ; 0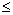 q
q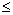 1; dx =D
zdq . Получим:
1; dx =D
zdq . Получим:
f(z+D z)-f(z)=D z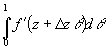 - формула Коши-Адамара.
- формула Коши-Адамара.
6) При
вычислении интеграла от аналитической функции контур интегрирования можно
деформировать так, чтобы он не выходил из области аналитичности подынтегральной
функции. Деформируя контур интегрирования так, как это допускается теоремой
Коши, можно легко вычислить многие интегралы.
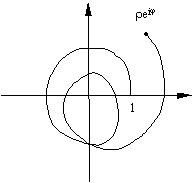
Важный пример. Вычислить интеграл dz/z , по контуру, изображенному на рисунке
справа. dz/z , по контуру, изображенному на рисунке
справа.
Обратим внимание на
то, что контур вообще не задан какой-либо формулой. Важны его
начальная и конечная точки и то, сколько раз он обходит вокруг
начала координат. |
 |
Нам нужно
разумно деформировать наш контур, чтобы интеграл подсчитывался легко.
Для этого заметим, что интеграл  dz/z легко вычисляется по
контурам двух типов:
dz/z легко вычисляется по
контурам двух типов:
во- первых вдоль действительной
оси: dz=dx,  =lnx (x>0); во-вторых, что менее очевидно, по дуге
окружности с центром в особой точке z=0 и радиусом r . На этой
окружности z=r eiq, dz=ir
eiqdq , так что
т dz/z=iт
dq . Поэтому
разумно деформировать наш контур в изображенный на рисунке справа,
где окружность с центром в нуле и радиуса r пробегается дважды
и еще по ней проходит дуга в j радиан. Ответ: наш интеграл равен
lnr +4p
i+ij =lnx (x>0); во-вторых, что менее очевидно, по дуге
окружности с центром в особой точке z=0 и радиусом r . На этой
окружности z=r eiq, dz=ir
eiqdq , так что
т dz/z=iт
dq . Поэтому
разумно деформировать наш контур в изображенный на рисунке справа,
где окружность с центром в нуле и радиуса r пробегается дважды
и еще по ней проходит дуга в j радиан. Ответ: наш интеграл равен
lnr +4p
i+ij |
 |
![]() C
C![]() (
(![]() ), g-односвязная, то
), g-односвязная, то ![]() f(z)dz =0.
f(z)dz =0. ![]() C
C![]() (g),
g-многосвязная, ограниченная извне контуром C0, а изнутри- контурами C1,
C2,...,Cn и пусть f(z)
(g),
g-многосвязная, ограниченная извне контуром C0, а изнутри- контурами C1,
C2,...,Cn и пусть f(z)![]() C
C![]() (
(![]() ). Тогда
). Тогда ![]() f(z)dz =0,
где С-полная граница g, С= C0
f(z)dz =0,
где С-полная граница g, С= C0![]() C1
C1![]() C2
C2![]() ...
...![]() Cn, проходящая в положительном
направлении.
Cn, проходящая в положительном
направлении. 
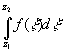 не зависит от
пути
не зависит от
пути  =F(z)- функция только z!
=F(z)- функция только z!
 =F(z)- называется неопределенным интегралом от f(z).
=F(z)- называется неопределенным интегралом от f(z).

 <e при
п D zп <d =>$
<e при
п D zп <d =>$![]() C(g). Тогда первообразной F(z) функции
f(z) в g называется " F(z)
C(g). Тогда первообразной F(z) функции
f(z) в g называется " F(z)![]() C
C![]() (g)
такая, что F '(z)=f(z).
(g)
такая, что F '(z)=f(z). ![]() C(g) и для
" замкнутого
контура g
C(g) и для
" замкнутого
контура g![]() g интеграл
g интеграл ![]() f(z)dz
=0, то
f(z)dz
=0, то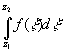 =F(z2)-F(z1);
где F- "
первообразная.
=F(z2)-F(z1);
где F- "
первообразная. ![]() (a,b).
(a,b). ![]() C
C![]() (g) и для " замкнутого контура g
(g) и для " замкнутого контура g![]() g
интеграл
g
интеграл ![]() f'(x )dx =0; f(z)- первообразная f '(z) =>
f'(x )dx =0; f(z)- первообразная f '(z) => ![]() =f(z+D z)-f(z). В качестве пути
интегрирования возьмем прямолинейный отрезок, соединяющий z и z+D z: x =z+D
zq ; 0
=f(z+D z)-f(z). В качестве пути
интегрирования возьмем прямолинейный отрезок, соединяющий z и z+D z: x =z+D
zq ; 0![]() q
q![]() 1; dx =D
zdq . Получим:
1; dx =D
zdq . Получим:
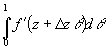 - формула Коши-Адамара.
- формула Коши-Адамара. 
