2. Интеграл вида I(z0)=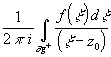 имеет смысл для " положения
точки z0 на
комплексной плоскости при условии, что z0 имеет смысл для " положения
точки z0 на
комплексной плоскости при условии, что z0 |
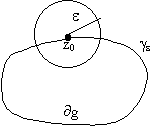 |
 f(x )dj =i
f(x )dj =i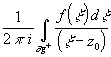 .
. 2. Интеграл вида I(z0)=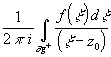 имеет смысл для " положения
точки z0 на
комплексной плоскости при условии, что z0 имеет смысл для " положения
точки z0 на
комплексной плоскости при условии, что z0 |
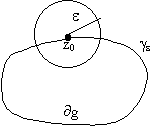 |
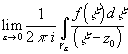 , где ge представляет собой часть контура
, где ge представляет собой часть контура 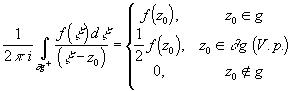
Следствия интегральной формулы Коши.
Пусть f(z)О
C![]() (g ).
(g ).
B>2.
Следствия: а) Формула среднего значения, б) Принцип максимума
модуля.
1 Формула среднего значения. Пусть
z0- некоторая внутренняя точка
односвязной области g. Возьмем окружность с центром в z0 и радиусом R, целиком лежащую в g. Тогда f
(z0)=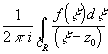 = (x = z0+R eij)=
= (x = z0+R eij)=![]()
![]() f(z0+Reij)dj =
f(z0+Reij)dj =![]()
![]() f(x )ds ,
f(x )ds ,
(ds=Rdj, круг KR![]() g)- формула среднего
значения.
g)- формула среднего
значения.
2. Принцип максимума
модуля.Если f(z)![]() C
C![]() (
(![]() ) и f(z)
) и f(z)![]() const, то |f(z)| достигает
своего максимального значения только на
const, то |f(z)| достигает
своего максимального значения только на ![]() .
.
Доказательство (от противного). Пусть $ z0![]() g:
|f(z0)|=M
g:
|f(z0)|=M ![]() |f(z)|,
для " z
|f(z)|,
для " z![]()
![]()
. M=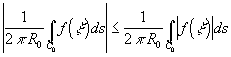
![]() M
=>
M
=> ![]() =M.
=M.
(C0-окружность
|z-z0|=R0, C0![]() g; x =
z0+R0eij,
ds=R0dj )=>|f(x
)|=M (для " x
g; x =
z0+R0eij,
ds=R0dj )=>|f(x
)|=M (для " x![]() C0). Действительно,
|f(x )|
C0). Действительно,
|f(x )| ![]() M для
" x
M для
" x![]() C0 по предположению. Далее, пусть в
некоторой точке x0
C0 по предположению. Далее, пусть в
некоторой точке x0![]() C0 выполнено |f(x0)|<M. Тогда,
т.к. |f(x )| непрерывен на C0 , то
$ дуга g0
C0 выполнено |f(x0)|<M. Тогда,
т.к. |f(x )| непрерывен на C0 , то
$ дуга g0
длины L0 -некоторая окрестность точки x0 (x0![]() g0), на которой |f(x )|
g0), на которой |f(x )|![]() M-e , e
>0 (а на остальной части окружности |f(x )| =M для " x
M-e , e
>0 (а на остальной части окружности |f(x )| =M для " x![]() C0/g0). Тогда
C0/g0). Тогда ![]()
![]()
![]() (M-e )L0/2pR0+M(2pR0-L0)/2pR0=M-e
L0/2pR0<M => M<M. Чего быть не может. =>
|f(x )|=M (для
"x
(M-e )L0/2pR0+M(2pR0-L0)/2pR0=M-e
L0/2pR0<M => M<M. Чего быть не может. =>
|f(x )|=M (для
"x![]() C0) => |f(x )|=M (x
C0) => |f(x )|=M (x![]() C': |z-z0|=R'<R0) => |f(x )|=M (x
C': |z-z0|=R'<R0) => |f(x )|=M (x![]() K0 : |z-z0|
K0 : |z-z0|![]() R0) =>
|f(z*)|=M для " z*
R0) =>
|f(z*)|=M для " z*![]() g.
g.
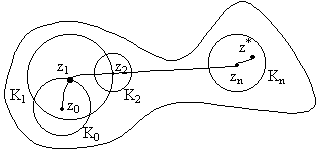 |
Покажем это.
Соединим точки z0 и
z* кривой L |z-z1| |
Замечания.
1. Если f(z)![]() C
C![]() (
(![]() ) и f(z)
) и f(z)![]() 0 для " z
0 для " z![]()
![]() , то имеет место принцип минимума модуля.
Для доказательства достаточно рассмотреть функцию j (z)=1/f(z) и воспользоваться
принципом максимума модуля
.
, то имеет место принцип минимума модуля.
Для доказательства достаточно рассмотреть функцию j (z)=1/f(z) и воспользоваться
принципом максимума модуля
.
2. Теорема верна
как для односвязной, так и для многосвязной области.
3. Геометрическая
интерпретация.
Действительные
функции двух действительных переменных u(x,y) и v(x,y)- вещественная и
мнимая части аналитической функции f(z) не
имеют в g локальных экстремумов, а могут иметь лишь седловые точки. Линии
равного уровня этих функций (если f![]() const) не замкнуты, т.е. упираются в границу
области g, либо уходят на бесконечность в случае неограниченной области. Внутри
области g нет точек, в которых эти функции возрастают или убывают по всем
направлениям.
const) не замкнуты, т.е. упираются в границу
области g, либо уходят на бесконечность в случае неограниченной области. Внутри
области g нет точек, в которых эти функции возрастают или убывают по всем
направлениям.
Важное обобщение.
| Назад | Вверх | Вперед |