1. Определение. F(z) - аналитическая функция комплексной переменной на всей комплексной плоскости кроме кривой C.
Пусть C- кусочно-гладкая кривая конечной длины L:
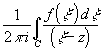 - интеграл типа Коши.
- интеграл типа Коши. Теорема 8.1. В " z0
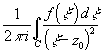 .
. Доказательство. Пусть z0 и z0+D z
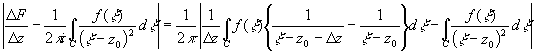 =
=
=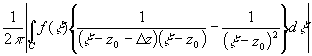 =
=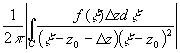
![]()
![]()
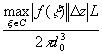 <e при |D z|<d <d 0=> $
<e при |D z|<d <d 0=> $![]() =F'(z0)=
=F'(z0)=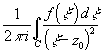 n.
n.
Замечание.
Непрерывность
F'(z), z![]() C доказывается аналогично с помощью оценки |D F'(z)|.
C доказывается аналогично с помощью оценки |D F'(z)|.
Теорема 8.2.
При z![]() C
F(z)
C
F(z)![]() C
C![]() (E\C). Уже
доказана.
(E\C). Уже
доказана.
2. Существование производных
всех порядков в области аналитичности функции комплексной
переменной.
Теорема 8.3. При zП C F(z) имеет непрерывные n-е производные для
" n, причем
F(n)(z)=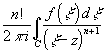 . Доказывается
методом математической индукции.
. Доказывается
методом математической индукции.
Теорема 8.4. (Основная!). Если f(z)![]() C
C![]() (g), то для
" n и
" z
(g), то для
" n и
" z![]() g $ f(n)(z)
g $ f(n)(z)![]() C
C![]() (g).
(g).
Доказательство. Пусть z0![]() g.
Построим замкнутый контур C, содержащий z0, который можно стянуть к z0, оставаясь все время в g. Тогда в силу интегральной формулы Коши
f(z0)=
g.
Построим замкнутый контур C, содержащий z0, который можно стянуть к z0, оставаясь все время в g. Тогда в силу интегральной формулы Коши
f(z0)=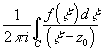 , но это интеграл типа Коши =>
$ f(n)(z0)=
, но это интеграл типа Коши =>
$ f(n)(z0)=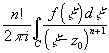 =>
f(n)(z0)
=>
f(n)(z0)![]() C
C![]() (g) для "
z0
(g) для "
z0![]() g n.
g n.
Итак, если функция f(z) является аналитической в g, то у
нее в g $
непрерывные производные всех порядков. Это существенное отличие от функции
действительной переменной имеющей непрерывную первую производную в некоторой
области, для которой из существования первой производной, вообще говоря, не
следует существование высших производных. Например, функция y(x)=x|x| непрерывна
на всей числовой прямой; ее производная y'(x)=2|x| также непрерывна на всей числовой прямой, однако, y"(0) не
существует .
Дальнейшие следствия
теоремы Коши
и интеграла Коши Теорема
Морера. Если f(z) Теорема
Лиувилля. Определение. Целая функция Важное замечание. Конфомное
отображение плоскости с выколотой точкой или расширенной плоскости на единичный
круг невозможно!
3.
Теоремы Морера и Лиувилля.
![]() C(g), g-односвязная и для " g
C(g), g-односвязная и для " g![]() g:
g: ![]() f(z)dz=0, где g -замкнутый контур, который
можно стянуть в точку, оставаясь в g, то f(z)
f(z)dz=0, где g -замкнутый контур, который
можно стянуть в точку, оставаясь в g, то f(z)![]() C
C![]() (g).
(g).
Доказательство. При условиях
теоремы $ F(z)=
![]() C
C![]() (g) (Теорема
6.1) , где z0 и z- произвольные точки g, а интеграл берется по
" пути
(g) (Теорема
6.1) , где z0 и z- произвольные точки g, а интеграл берется по
" пути![]() g, соединяющему эти точки. При этом
F'(z)=f(z). Но производная аналитической функции сама является аналитической
функцией (Теорема 8.4)
, т.е. $
F"(z)
g, соединяющему эти точки. При этом
F'(z)=f(z). Но производная аналитической функции сама является аналитической
функцией (Теорема 8.4)
, т.е. $
F"(z)![]() C(g) а именно F"(z)=f'(z)
C(g) а именно F"(z)=f'(z)![]() C(g).n
C(g).n
Замечание.
1. Теорема Морера является в некотором
смысле обратной к теореме
Коши.
2. Теорема 8.4 и Теорема Морера справедливы и для многосвязных
ообластей.
Если f(z)![]() C
C![]() (E) и f(z)
(E) и f(z)![]() const, то при z
const, то при z![]()
![]() , |f(z)|
, |f(z)|![]()
![]() .
.
Другая формулировка:
Если f(z)![]() C
C![]() (E) и $
M: |f(z)|
(E) и $
M: |f(z)|![]() M для " z (|f(z)|- равномерно ограничен), то f(z)
M для " z (|f(z)|- равномерно ограничен), то f(z)![]() const.
const.
Доказательство. f'(z)=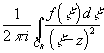 ., где CR: |x -z|=R. По условию теоремы
$ M:
., где CR: |x -z|=R. По условию теоремы
$ M:
|f(z)|![]() M, независимо от R => |f'(z)|
M, независимо от R => |f'(z)|![]() 2p RM/2p R2=M/R. Т.к. R можно выбрать сколь угодно большим (R
2p RM/2p R2=M/R. Т.к. R можно выбрать сколь угодно большим (R![]()
![]() ), а f'(z) не зависит от R, то |f'(z)|=0. В
силу произвольности выбора z, |f'(z)|=0 на всей комплексной плоскости
E=>f(z)
), а f'(z) не зависит от R, то |f'(z)|=0. В
силу произвольности выбора z, |f'(z)|=0 на всей комплексной плоскости
E=>f(z)![]() const для
" z.n
const для
" z.n
f(z)![]() C
C![]() (E)(на всей комплексной плоскости) (z
(E)(на всей комплексной плоскости) (z![]()
![]() ) называется целой
функцией.
) называется целой
функцией.
![]() const не может быть ограничена по абсолютной
величине.
const не может быть ограничена по абсолютной
величине.
Так например, целые функции
sin z и cos z неограничены по модулю!
Пример целой функции. Функция
f(z)=zn.
Отображение области однолистности
Сектор раскрыва 2p /n отображается на всю комплексную плоскость.
| Назад | Вверх | Вперед |