Лекция 5.
- § 9. Интегралы, зависящие от
параметра.
- 1. Понятие интеграла, зависящего от
параметра. Достаточные условия существования.
- 2. Основная теорема
F(z)ОC
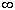 (g).
(g).
1. Понятие интеграла, зависящего от параметра.
Достаточные условия существования.
Пусть на комплексной плоскости Z
заданы: кусочно-гладкий контур C конечной длины  ds=L, область g, и функция двух комплексных
переменных w=j (z,x ), z
ds=L, область g, и функция двух комплексных
переменных w=j (z,x ), z  g, x
g, x  C, удовлетворяющая следующим условиям:
C, удовлетворяющая следующим условиям:
1. Для " x0  C j(z,x0)=f(z)
C j(z,x0)=f(z)  C
C 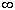 (g),
т.е. $
(g),
т.е. $ 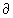 j/
j/ 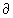 z(z,x0)
z(z,x0)  C
C 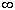 (g).
(g).
2. j(z,x )- непрерывна по
совокупности переменных. Т.е. "e>0 $d(e,
z,x)>0:
|j( z+D z,x+Dx)-j( z,x) |<e при |D z|,|Dx |<d .
3.
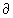 j /
j / 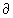 z(z,x ),┘,
z(z,x ),┘, 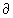 nj/
nj/ 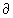 zn(z,x )-
также непрерывны по совокупности переменных.
zn(z,x )-
также непрерывны по совокупности переменных.
Замечание. Из 2 следует, что j(z,x ) непрерывна по z в "z  g
равномерно по x,т.е. для фиксированного z0
g
равномерно по x,т.е. для фиксированного z0
 g и "e>0 $d(e,
z0)>0 такое, что |j( z0+D z,x)-j( z0,x) |<e
g и "e>0 $d(e,
z0)>0 такое, что |j( z0+D z,x)-j( z0,x) |<e
при |D z|<d для всех x  C одновременно.
C одновременно.
Доказательство. От
противного, аналогично доказательству равномерной непрерывности в замкнутой
области ( Теорема 3.1).
Аналогичное утверждение справедливо и для 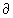 j/
j/ 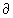 z(z,x ).
z(z,x ).
2. Основная теорема F(z)ОC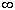 (g).
(g).
Теорема 9.1 Если j(z,x ), z  g, x
g, x  C удовлетворяет условиям 1-3, то интеграл, зависящий
от параметра z $ и является аналитической функцией z в
области g.
C удовлетворяет условиям 1-3, то интеграл, зависящий
от параметра z $ и является аналитической функцией z в
области g.
 j(z,x )dx
=F(z)
j(z,x )dx
=F(z)  C
C 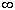 (g) и F(n)(z)=
(g) и F(n)(z)= 
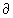 nj/
nj/ 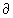 zn(z,x )dx .
zn(z,x )dx .
Доказательство.
Разобьем доказательство на 3 этапа:
1. Докажем, что F(z)  C(g).
C(g).
|D F|=|F(z+D z)-F(z)|=|  [j (z+D z,x )-j (z,x
)]dx |
[j (z+D z,x )-j (z,x
)]dx | 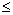 L
L
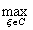 |j(z+D z,x )-j (z,x
)|<
|j(z+D z,x )-j (z,x
)|<
<( по замечанию к условию 2 ) < Le
'<e как только |D
z|<d(e) .
2. Докажем,
что $ 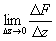 =F'(z)=
=F'(z)= 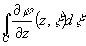 .
.
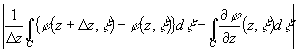
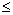
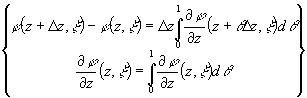
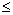
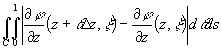 <
<
<( по замечанию к условию 2 ) < Le '<e как только |D z|<d(e) .
3. Докажем, что
F'(z)  C(g). Доказательство аналогично
п.1.
C(g). Доказательство аналогично
п.1.
Итак, F(z)  C
C 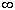 (g) и
F(n)(z)=
(g) и
F(n)(z)= 
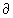 nj/
nj/ 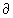 zn(z,x
)dx . n
zn(z,x
)dx . n
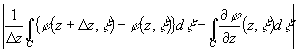
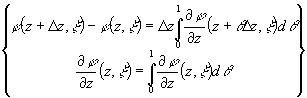
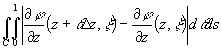 <
<