Доказательство. Необходимость. Если ряд сходится, то |rn|=|S-Sn|
Достаточность. |Sn+m-Sn|=|
Т.к. rn+m-rn=![]() ak=Sn+m-Sn, то необходимым и достаточным признаком
сходимости числового ряда является стремление |rn|
ak=Sn+m-Sn, то необходимым и достаточным признаком
сходимости числового ряда является стремление |rn|![]() 0 при n
0 при n![]()
![]() .
.
Доказательство. Необходимость. Если ряд
сходится, то |rn|=|S-Sn|![]() 0.
0.
Достаточность.
|Sn+m-Sn|=|![]() ak|=|rn+m-rn|.
Пусть |rn|
ak|=|rn+m-rn|.
Пусть |rn|![]() 0 => Для "e>0 $ N(e ): |rn|<e /2 для "n
0 => Для "e>0 $ N(e ): |rn|<e /2 для "n![]() N=>|rn+m|<e /2 для "n
N=>|rn+m|<e /2 для "n![]() N и "m>0
=>|Sn+m-Sn|=|rn+m-rn|<e => ряд
сходится.n
N и "m>0
=>|Sn+m-Sn|=|rn+m-rn|<e => ряд
сходится.n
Определение. Если ![]() |ak|<
|ak|<![]() (сходится) , то ряд называется
абсолютно сходящимся.
(сходится) , то ряд называется
абсолютно сходящимся.
Очевидно, что если ряд сходится абсолютно, то он
сходится. Обратное, вообще говоря, неверно. Например, ряд ![]() (-1)k/k сходится, тогда как
ряд
(-1)k/k сходится, тогда как
ряд ![]() 1/k- расходится,
1/k- расходится,
Достаточными критериями абсолютной сходимости
рядов являются признаки Даламбера и Коши.
Признак
Даламбера. Если начиная с некоторого номера N выполняется
неравенство |an+1/an|![]() L<1 для "n
L<1 для "n![]() N, то ряд
N, то ряд ![]() |ak|
сходится.
|ak|
сходится.
Если начиная с некоторого N
|an+1/an|![]() 1
для "n
1
для "n![]() N, то
ряд
N, то
ряд ![]() ak расходится.
ak расходится.
Признак Даламбера в
предельной форме.
Если $ ![]() |an+1/an|=L, то при
L<1 ряд
|an+1/an|=L, то при
L<1 ряд ![]() |ak| сходится, при L>1 ряд
|ak| сходится, при L>1 ряд![]() ak расходится,при L=1 ничего сказать нельзя.
ak расходится,при L=1 ничего сказать нельзя.
Доказательство. Если L<1, то $e>0: L<1-2e =>L+e <1-e. Т.к. $![]() |an+1/an|=L, то $ N:
|an+1/an|=L, то $ N:
L-e
<|an+1/an|< L+e <1-e =q<1, для " n![]() N
=>|an+1|<|an|q<┘<|aN|qn+1-N,
т.е. ряд мажорируется геометрической прогрессией со
знаменателем q<1.n
N
=>|an+1|<|an|q<┘<|aN|qn+1-N,
т.е. ряд мажорируется геометрической прогрессией со
знаменателем q<1.n
Аналогично доказывается расходимость ряда при
L>1.
Признак Коши.
Если начиная с некоторого N Если ряд сходится в g, то "e>0 $ N(e,z): | rn(z)|
<e для "n Необходимый и достаточный признак
сходимости: Необходимое и достаточное условие равномерной
сходимости- критерий Коши: Достаточный
признак равномерной сходимости Вейерштрасса. (Мажорантный признак
Вейерштрасса). ![]()
![]() L<1
для "n
L<1
для "n![]() N, то
ряд
N, то
ряд ![]() |ak| сходится.
|ak| сходится.
Если начиная с некоторого N ![]()
![]() 1 для "n
1 для "n![]() N, то ряд
N, то ряд ![]() ak расходится.
ak расходится.
Признак Коши в
предельной форме.
Если $ ![]()
![]() =L, то при
L<1 ряд
=L, то при
L<1 ряд ![]() |ak|
сходится,при L>1
ряд
|ak|
сходится,при L>1
ряд![]() ak расходится,при L=1 ничего сказать нельзя.
ak расходится,при L=1 ничего сказать нельзя.
Доказательство. Если L<1, то $e>0: L<1-2e =>L+e <1-e. Т.к. $![]()
![]() =L, то $N:
=L, то $N:
L-e <![]() <L+e <1-e =q<1, n
<L+e <1-e =q<1, n![]() N,
q<1=>|an|<qn, т.е.
ряд мажорируется геометрической прогрессией со знаменателем q<1.n
N,
q<1=>|an|<qn, т.е.
ряд мажорируется геометрической прогрессией со знаменателем q<1.n
Аналогично доказывается расходимость ряда при
L>1.
2. Понятие функционального
ряда.
Пусть дана
последовательность ![]() , z
, z![]() g. Выражение
g. Выражение ![]() uk(z)-
называется функциональным рядом,
заданным в g.
uk(z)-
называется функциональным рядом,
заданным в g.
Определение.Если при " z![]() g,
соответствующий числовой ряд сходится к определенному комплексному числу w(z),
то в g определена f(z)=w, которая называется суммой функционального
ряда, а сам ряд называется
сходящимся в g.
g,
соответствующий числовой ряд сходится к определенному комплексному числу w(z),
то в g определена f(z)=w, которая называется суммой функционального
ряда, а сам ряд называется
сходящимся в g.
![]() N(e ,z).
N(e ,z).
Критерий Коши:
для "e>0 $
N(e ,z): | Sn+m(z)-Sn(z)|
<e для "n![]() N и "m>0.
N и "m>0.
Вообще говоря, в каждой точке z![]() g N свое:
N=N(e ,z) и общего
N для всей z может и не существовать.
g N свое:
N=N(e ,z) и общего
N для всей z может и не существовать.
3. Равномерная сходимость еun(z) в области g.
Если для "e>0
$ N(e) что | rn(z)| <e для "n![]() N(e) и " z одновременно, то ряд
.
N(e) и " z одновременно, то ряд
.![]() uk(z) называется
равномерно сходящимся к функции f(z) в g.
uk(z) называется
равномерно сходящимся к функции f(z) в g.
Обозначение: ![]() uk(z)=>f(z).
uk(z)=>f(z).
Понятие равномерной сходимости-глобальное.
Если
для "e>0 $
N(e ): | Sn+m(z)-Sn(z)|
<e для "n![]() N и "m>0 и " z одновременно, то ряд .
N и "m>0 и " z одновременно, то ряд .![]() uk(z)=>f(z).
uk(z)=>f(z).
Доказательство.
Необходимость. Пусть ряд ![]() uk(z)
сходится равномерно к f(z): "e >0 $ N(e)
что |f(z)-Sn(z)| <e /2 для "n
uk(z)
сходится равномерно к f(z): "e >0 $ N(e)
что |f(z)-Sn(z)| <e /2 для "n![]() N(e) и "z
N(e) и "z![]() g => и подавно
|f(z)-Sn+m(z)| <e /2 =>
g => и подавно
|f(z)-Sn+m(z)| <e /2 =>
=>| Sn+m(z)-Sn(z)| <e
для "n![]() N и "m>0 и "z
N и "m>0 и "z![]() g.
g.
Достаточность. Пусть для "e>0 $ N(e ): | Sn+m(z)-Sn(z)| <e (*) для "n![]() N и "m>0 и "z
N и "m>0 и "z![]() g => в "z
g => в "z![]() g выполнен критерий Коши для числового ряда, т.е. все
числовые ряды сходятся и в g определена
f(z)=
g выполнен критерий Коши для числового ряда, т.е. все
числовые ряды сходятся и в g определена
f(z)=![]() uk(z). Переходя в
(*) к пределу при m
uk(z). Переходя в
(*) к пределу при m![]()
![]() получим |f(z)-Sn(z)|
получим |f(z)-Sn(z)|![]() e для "n
e для "n![]() N(e) и "z
N(e) и "z![]() g => |rn(z)| <e для "n
g => |rn(z)| <e для "n![]() N(e) и "z
N(e) и "z![]() g. n
g. n
Если
|uk(z)|<ak, ak>0 для "k![]() N и
"z
N и
"z![]() g и
g и ![]() ak<
ak<![]() (сходится),
то
(сходится),
то ![]() uk(z)=>f(z) в
g.
uk(z)=>f(z) в
g.
Доказательство.
|rn(z)| =|![]() uk(z)|
uk(z)|![]()
![]() |uk(z)|<
|uk(z)|<![]() ak<e
для "n
ak<e
для "n![]() N(e) и "z
N(e) и "z![]() g. n
g. n
4. Свойства равномерно
сходящихся рядов. Непрерывность суммы. Возможность почленного интегрирования.
Теорема Вейерштрасса. II теорема Вейерштрасса.
Свойства равномерно сходящихся рядов:
1) Пусть uk(z)![]() С(g) и
С(g) и ![]() uk(z)=>f(z), тогда f(z)
uk(z)=>f(z), тогда f(z)![]() С(g).
С(g).
Доказательство. |D
f|=|f(z+D z)-f(z)|![]() |f(z+D z)-Sn(z+D z)|+|Sn(z+D
z)-Sn(z)|+|Sn(z)-f(z)|?
|f(z+D z)-Sn(z+D z)|+|Sn(z+D
z)-Sn(z)|+|Sn(z)-f(z)|? ![]() e /3+e /3+e /3=e
для |D
z|<d , n
e /3+e /3+e /3=e
для |D
z|<d , n![]() N.n
N.n
2). Пусть
uk(z)![]() С(g) и
С(g) и ![]() uk(z)=>f(z). Пусть С кусочно- гладкий контур C
uk(z)=>f(z). Пусть С кусочно- гладкий контур C![]() g конечной
длины L:
g конечной
длины L: ![]() ds=L, тогда
ds=L, тогда![]() f(z)dz=
f(z)dz=![]()
![]() uk(z)dz.
uk(z)dz.
Доказательство |![]() f(z)dz-
f(z)dz-![]()
![]() uk(z)dz |=|
uk(z)dz |=|![]() rn(z)dz |
rn(z)dz |![]()
![]() | rn(z) |
ds<e 'L<en
| rn(z) |
ds<e 'L<en
3) Теорема
Вейерштрасса. Если uk(z)![]() C
C![]() (g) и
(g) и ![]() uk(z)=>f(z), для
"z
uk(z)=>f(z), для
"z![]() "
"![]() '
'![]() g,
g,
(для любой замкнутой
подобласти области g) то:
1. f(z)![]() C
C![]() (g).
(g).
2.
f(p)(z)=![]() uk(p)(z), для
"z
uk(p)(z), для
"z![]() g.
g.
3. ![]() uk(p)(z)=>f(p)(z), для "z
uk(p)(z)=>f(p)(z), для "z![]() "
"![]() '
'![]() g.
g.
Доказательство
1. Рассмотрим " ![]() '
'![]() g и C- замкнутый
контур: С
g и C- замкнутый
контур: С![]()
![]() ', стягивающийся в точку z
', стягивающийся в точку z![]()
![]() '. Т.к. uk(z)
'. Т.к. uk(z)![]() C
C![]() (g) и
(g) и ![]() uk(z)
равномерно сходится к f(z) для "z
uk(z)
равномерно сходится к f(z) для "z![]()
![]() ', то f(z) непрерывна в
', то f(z) непрерывна в ![]() ' (по
свойству 1). По свойству 2
' (по
свойству 1). По свойству 2
![]()
![]()
![]() uk(z)dz= (по теореме Коши) =
uk(z)dz= (по теореме Коши) =![]() 0=0. Тем самым выполнены условия теоремы Морера =>
f(z)
0=0. Тем самым выполнены условия теоремы Морера =>
f(z)![]() C
C![]() (
(![]() '). =>
в силу произвольности
'). =>
в силу произвольности ![]() ' => f(z)
' => f(z)![]() C
C![]() (g).
(g).
Замечание. Т.к.
rn(z)=f(z)- Sn(z) => rn(z)![]() C
C![]() (g).
(g).
2. Рассмотрим
"![]() '
'![]() g и C- замкнутый
контур: С
g и C- замкнутый
контур: С![]()
![]() ', стягивающийся в точку z
', стягивающийся в точку z![]()
![]() '. Т.к. f(z)
'. Т.к. f(z)![]() C
C![]() (g), то f(p)(z)=
(g), то f(p)(z)=![]() . =(по теореме 8.4) =(т.к.
. =(по теореме 8.4) =(т.к.![]() uk(x )|x
uk(x )|x![]() C=>f(x )|x
C=>f(x )|x![]() C =>
C => )=
)=![]() =
= ![]() uk(p)(z).
uk(p)(z).
Замечание.
rn(p)(z)=f(p)(z)-Sn(p)(z)=![]() uk(p)(z).
uk(p)(z).
3. Рассмотрим "![]() '
'![]() g и C- замкнутый
контур, содержащий
g и C- замкнутый
контур, содержащий ![]() ' внутри, и такой, что для"z
' внутри, и такой, что для"z![]()
![]() ' и "x
' и "x![]() С выполнено
неравенство |z-x|>d0. Тогда
rn(p)(z)=
С выполнено
неравенство |z-x|>d0. Тогда
rn(p)(z)=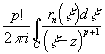 .
.
|rn(x )|<e', n> N(e') (т.к. C граница замкнутой подобласти ![]() ''
''![]() g). |rn(p)(z)|
g). |rn(p)(z)|![]()
![]() <e для "z
<e для "z![]()
![]() ' одновременно =>
' одновременно => ![]() uk(p)(z)=>f(p)(z), для "z
uk(p)(z)=>f(p)(z), для "z![]() "
"![]() '
'![]() g.n
g.n
Замечание. Даже если ![]() uk(z)=>f(z) при z
uk(z)=>f(z) при z![]()
![]() , то все равно мы
можем доказать равномерную сходимость ряда из производных лишь в любой
замкнутой подобласти
, то все равно мы
можем доказать равномерную сходимость ряда из производных лишь в любой
замкнутой подобласти ![]() 'области g. Т.е.
'области g. Т.е.![]() uk(p)(z)=>f(p)(z), лишь для "z
uk(p)(z)=>f(p)(z), лишь для "z![]() "
"![]() '
'![]() g. Из равномерной
сходимости ряда
g. Из равномерной
сходимости ряда ![]() uk(z)=>f(z) z
uk(z)=>f(z) z![]()
![]() не следует! равномерная
сходимость в этой области ряда составленного из производных.!
не следует! равномерная
сходимость в этой области ряда составленного из производных.!
Пример. Ряд![]() zk/k2
сходится равномерно в круге |z|
zk/k2
сходится равномерно в круге |z| ![]() 1, а ряд из производных
1, а ряд из производных ![]() zk-1/k
не может равномерно сходится в круге |z|
zk-1/k
не может равномерно сходится в круге |z|![]() 1 , т.к. он расходится
при z=1. Ряд
1 , т.к. он расходится
при z=1. Ряд ![]() zk-1/k равномерно сходится при |z|<1.
zk-1/k равномерно сходится при |z|<1.
II Теорема
Вейерштрасса. Пусть
uk(z)![]() C
C![]() (
(![]() )
и
)
и ![]() uk(x )=>f(x ), для x
uk(x )=>f(x ), для x![]() g. Тогда
g. Тогда ![]() uk(z)=>f(z), z
uk(z)=>f(z), z![]()
![]() .
.
Доказательство |Sn+m(x )-Sn(x )| <e для "x![]() g =>
|Sn+m(z)-Sn(z)| <eдля "z
g =>
|Sn+m(z)-Sn(z)| <eдля "z![]()
![]() √ в силу принципа максимума.) n
√ в силу принципа максимума.) n
| Назад | Вверх | Вперед |