Лекция 7.
- §13. Понятие аналитического
продолжения.
- 1.Аналитическое
продолжение через общую подобласть двух областей.
- 2. Теорема. На границе
круга сходимости степенного ряда найдется хотя бы одна особая точка
аналитической функции комплексной переменной - суммы ряда
- 3. Аналитическое
продолжение через общий участок границы двух областей.
1. Аналитическое
продолжение через общую подобласть двух областей.
Пусть f 1(z) C
C (g1 ) и g 1
(g1 ) и g 1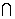 g2=g12
g2=g12
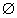 и пусть f 2(z)
и пусть f 2(z) C
C (g2 ), причем f
2(z)
(g2 ), причем f
2(z) f1(z), z
f1(z), z g12 . Тогда f
2 (z) называется
аналитическим продолжением f1 (z) на g2 через общую подобласть g 12.
g12 . Тогда f
2 (z) называется
аналитическим продолжением f1 (z) на g2 через общую подобласть g 12.
В силу
теоремы единственности определенной
аналитической функции если аналитическое
продолжение $ , то
оно- единственно. При этом в g=g 1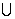 g2 $!
(единственная) аналитическая функция
F(z)=
g2 $!
(единственная) аналитическая функция
F(z)=
 C
C (g). F(z)
называется аналитическим продолжением своего первоначального элемента f
1(z)
(g). F(z)
называется аналитическим продолжением своего первоначального элемента f
1(z) C
C (g1 ) на большую область g, для которой g 1
(g1 ) на большую область g, для которой g 1 g
– подобласть.
g
– подобласть.
Осуществить
аналитическое продолжение можно с помощью степенных рядов. Пусть f(z) C
C (g) и z
0
(g) и z
0 g- правильная точка g, т.е. $
g- правильная точка g, т.е. $  cn(z-z0)n сходящийся к f(z) в общей части g и круга
сходимости степенного ряда |z-z 0| < r
(z0 ). Если r (z0 ) больше
расстояния от точки z 0 до
cn(z-z0)n сходящийся к f(z) в общей части g и круга
сходимости степенного ряда |z-z 0| < r
(z0 ). Если r (z0 ) больше
расстояния от точки z 0 до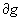 , то круг сходимости выйдет за
пределы g, и мы получим F(z)- аналитическое продолжение f(z)
, то круг сходимости выйдет за
пределы g, и мы получим F(z)- аналитическое продолжение f(z) C
C (g) на большую
область g
(g) на большую
область g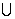 |z-z0|< r (z0).
|z-z0|< r (z0).
2. Теорема. На границе круга
сходимости степенного ряда найдется хотя бы одна особая точка аналитической
функции комплексной переменной - суммы ряда.
Теорема 13.1 На границе круга сходимости степенного ряда найдется хотя бы
одна особая точка аналитической функции
комплексной переменной, которая (функция) является суммой ряда внутри его круга
сходимости |z-z 0|<R0.
Доказательство (от противного). Предположим,
что " x : | x -z0|=R0 являются правильными точками f(z)= cn(z-z0)n, f(z)
cn(z-z0)n, f(z) C
C (|z-z0| <R0 )
т.е. для "x
(|z-z0| <R0 )
т.е. для "x
$
r ( x )>0:  cn( x )(z- x )n =f(z) в общей части |z-z 0|
<R0
cn( x )(z- x )n =f(z) в общей части |z-z 0|
<R0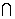 | x -z0|< r ( x ).
| x -z0|< r ( x ).
Докажем, что
r ( x )>0 является непрерывной функцией x на C R0 и
даже
Липшиц- непрерывной: т.е. |
r ( x 1)- r ( x 2)| | x 1- x 2|.
| x 1- x 2|.
Предположим
противное. Пусть r ( x
1)> r ( x
2 ) и $
d>0 : r ( x 1)> r ( x 2)+| x 1- x 2|+
d (*).
Это
означает, что круг |z- x
2|< r ( x 2 )
лежит внутри круга |z- x
1|< r ( x 1 ). Но
в общей части трех кругов |z-z0|<R0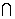 |z- x 1|< r (
x 1) |z- x 1|< r (
x 1)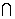 |z- x
2|< r ( x 2 ) все
три степенных ряда сходятся к одной и той же f(z) |z- x
2|< r ( x 2 ) все
три степенных ряда сходятся к одной и той же f(z) C C (|z-z0|<R0
) =>степенной ряд (|z-z0|<R0
) =>степенной ряд cn( x 2)(z-
x 2)n может быть продолжен на большую область, т.е.
он сходится в круге
cn( x 2)(z-
x 2)n может быть продолжен на большую область, т.е.
он сходится в круге |
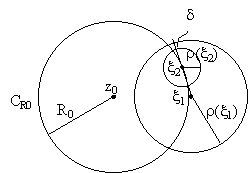 |
радиуса r ( x 2 ), который не
меньше чем расстояние от x 2
до границы круга |z- x
1|< r ( x
1) => r ( x
2) r ( x 1)-| x 1- x 2 |, но тогда из (*) =>
r ( x 1)>
r ( x 1)+ d и т.к. d >0 мы пришли к абсурдному
заключению. Но это противоречие явилось следствием нашего предположения о том,
что r ( x ) не
является Липшиц- непрерывной на C R0 .
Итак: | r ( x
1)- r ( x
2)|
r ( x 1)-| x 1- x 2 |, но тогда из (*) =>
r ( x 1)>
r ( x 1)+ d и т.к. d >0 мы пришли к абсурдному
заключению. Но это противоречие явилось следствием нашего предположения о том,
что r ( x ) не
является Липшиц- непрерывной на C R0 .
Итак: | r ( x
1)- r ( x
2)| | x 1- x
2|.
| x 1- x
2|.
Из Липшиц- непрерывности =
> простая непрерывность. А т.к. непрерывная функция r ( x )>0 на замкнутом множестве | x -z0|=R0 достигает своей нижней грани, т.е. $x* :
r ( x ) r ( x * ) для "x
r ( x * ) для "x CR0 .
Но по предположению для "x
CR0 .
Но по предположению для "x CR0 r (
x )>0=> r ( x *)= r 0
>0. Из того, что r
( x )
CR0 r (
x )>0=> r ( x *)= r 0
>0. Из того, что r
( x ) r 0 следует,
что функция f(z)=
r 0 следует,
что функция f(z)= cn(z-z0)n при |
z-z0|<R0 может быть
аналитически продолжена в круг |z-z 0|<R0+ r 0 , а
следовательно, радиус сходимости исходного степенного ряда не R
0 , а R 0+
r 0 . Но это
противоречит условиям теоремы.
cn(z-z0)n при |
z-z0|<R0 может быть
аналитически продолжена в круг |z-z 0|<R0+ r 0 , а
следовательно, радиус сходимости исходного степенного ряда не R
0 , а R 0+
r 0 . Но это
противоречит условиям теоремы.
К этому
противоречию мы пришли, предположив, что все точки x CR0
- правильные. = > На C R0
имеется хотя бы одна точка x ** , являющаяся
особой, т.е. r ( x
**)=0. n
CR0
- правильные. = > На C R0
имеется хотя бы одна точка x ** , являющаяся
особой, т.е. r ( x
**)=0. n
Следствие.
Радиус круга сходимости определяется расстоянием от центра сходимости
до ближайшей особой точки той аналитической функции, к которой сходится данный
ряд.
Примеры.
1.  (-1)nz2n=
(-1)nz2n= (-z2)n=1/(1+z2);
|z|<1.
(-z2)n=1/(1+z2);
|z|<1.
Особые точки суммы ряда
очевидно z 1,2= ± i. Отсюда понятно, почему разложение функции f(x)= 1/(1+x
2 ) в степенной ряд в окрестности
точки x=0 абсолютно сходится только при -1<x<1, условно сходится при |x|=
1 и расходится при|x|>1, хотя эта функция при "
x обладает непрерывными и ограниченными
производными " порядка.
2. Степенной ряд, сумма которого имеет
счетное, всюду плотное множество особых точек на границе своего круга
сходимости.
 - сходится при |z|<1 (по
формуле Коши- Адамара ).
- сходится при |z|<1 (по
формуле Коши- Адамара ).
При z=1 ряд
расходится. Рассмотрим точки 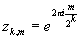 , |zk,m|=1; k-фиксировано,
m=0,1,2....; m=0, z k,0=1; m=2k ,
, |zk,m|=1; k-фиксировано,
m=0,1,2....; m=0, z k,0=1; m=2k ,  =1, при m=1,... ,2 k -1 точки делят окружность единичного радиуса на 2
k частей.
=1, при m=1,... ,2 k -1 точки делят окружность единичного радиуса на 2
k частей.
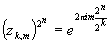 и при n
и при n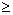 k
k 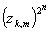 =1=> в этих точках ряд расходится.
=1=> в этих точках ряд расходится.
При k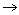
 точки z k,m всюду плотно расположены на единичной окружности
точки z k,m всюду плотно расположены на единичной окружности
Таким образом, сумма ряда имеет
счетное, всюду плотное множество особых точек на границе единичного круга = >
Эту аналитическую функцию нельзя аналитически продолжить за границу единичного
круга !!. (Т.к. в " z: |z|<1 радиус круга сходимости степенного ряда будет
не больше расстояния до границы единичного круга. По следствию к теореме 13.1
3. Аналитическое
продолжение через общий участок границы двух областей.
Теорема 13.2
Пусть fi(z) C
C (gi ),
i=1,2 и f i(z)
(gi ),
i=1,2 и f i(z) C
C (gi+ G ) и f 1|
G = f2| G . Тогда F(z)=
(gi+ G ) и f 1|
G = f2| G . Тогда F(z)=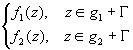
 C
C (g=g1+g2+ G
).
(g=g1+g2+ G
).
Доказательство .
Достаточно показать, что " z0 G является правильной точкой F(z) (кроме может быть
концевых точек G ).
Возьмем " z0
G является правильной точкой F(z) (кроме может быть
концевых точек G ).
Возьмем " z0 G и построим
G и построим
C=C
1( g1)+C2(
g1)+C2( g2); C
g2); C g- кусочно-
гладкие. Рассмотрим интеграл типа Коши
g- кусочно-
гладкие. Рассмотрим интеграл типа Коши
F (z)=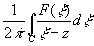  C C (g' (g' g).
Поскольку при z g).
Поскольку при z C F (z)
непрерывна на C, то z 0 - правильная точка F
(z). Пусть
C F (z)
непрерывна на C, то z 0 - правильная точка F
(z). Пусть
z 1 g'1 . Тогда F
(z1)= g'1 . Тогда F
(z1)=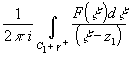 + +
+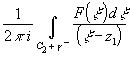 .
Второе слагаемое равно 0 т.к. z 1 .
Второе слагаемое равно 0 т.к. z 1 g'1. => F (z1)=F(z1 ). g'1. => F (z1)=F(z1 ). |
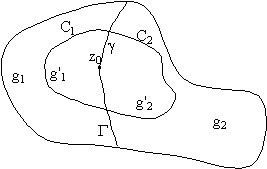 |
Аналогично получим, что при z 2 g'2 F
(z2)=F(z2 ). По
непрерывности получим, что F(z 0)= F
(z0) => z0
g'2 F
(z2)=F(z2 ). По
непрерывности получим, что F(z 0)= F
(z0) => z0 G является правильной точкой F(z). n
G является правильной точкой F(z). n
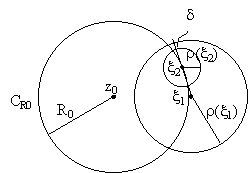

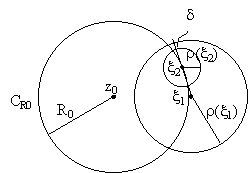
![]() и при n
и при n![]() k
k ![]() =1=> в этих точках ряд расходится.
=1=> в этих точках ряд расходится. ![]()
![]() точки z k,m всюду плотно расположены на единичной окружности
точки z k,m всюду плотно расположены на единичной окружности
![]() C
C![]() (gi ),
i=1,2 и f i(z)
(gi ),
i=1,2 и f i(z)![]() C
C![]() (gi+ G ) и f 1|
G = f2| G . Тогда F(z)=
(gi+ G ) и f 1|
G = f2| G . Тогда F(z)=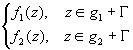
![]() C
C![]() (g=g1+g2+ G
).
(g=g1+g2+ G
).![]() G является правильной точкой F(z) (кроме может быть
концевых точек G ).
Возьмем " z0
G является правильной точкой F(z) (кроме может быть
концевых точек G ).
Возьмем " z0![]() G и построим
G и построим ![]() g1)+C2(
g1)+C2(![]() g2); C
g2); C![]() g- кусочно-
гладкие. Рассмотрим интеграл типа Коши
g- кусочно-
гладкие. Рассмотрим интеграл типа Коши
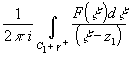 +
+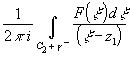 .
Второе слагаемое равно 0 т.к. z 1
.
Второе слагаемое равно 0 т.к. z 1