Лекция 6.
- §12. Единственность определения
аналитической функции.
- 1. Понятие правильной точки.
- 2. Нули аналитической функции.
- 3.Теорема единственности определенной
аналитической функции.
1. Понятие правильной
точки.
Пусть f(z) задана в g, за
исключением может быть некоторых изолированных точек.
Точка z 0 g называется
правильной точкой функции f(z), заданной в g,
если $
g называется
правильной точкой функции f(z), заданной в g,
если $ cn(z-z0)n =f(z) в g
cn(z-z0)n =f(z) в g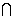 |z-z0| < r
(z0 ), где r (z0 )-радиус сходимости степенного ряда.
|z-z0| < r
(z0 ), где r (z0 )-радиус сходимости степенного ряда.
Все остальные точки z g- особые
точки функции f(z), заданной в g.
g- особые
точки функции f(z), заданной в g.
Замечание. Если f(z) C
C (g), то все z
(g), то все z g- правильные точки f(z). Если
f(z) задана в
g- правильные точки f(z). Если
f(z) задана в 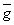 ,
то граничные точки могут быть как правильными, так и особыми.
,
то граничные точки могут быть как правильными, так и особыми.
2. Нули аналитической
функции.
Пусть f(z) C
C (g);
f(z0)=0, z0
(g);
f(z0)=0, z0 g,
тогда z0 - нуль
аналитической функции . f(z)=
g,
тогда z0 - нуль
аналитической функции . f(z)= cn(z-z0)n
=> c0 =0. Если c
1=…= cn-1 =0, а
c n
cn(z-z0)n
=> c0 =0. Если c
1=…= cn-1 =0, а
c n 0, то z 0 - нуль n-того порядка.
0, то z 0 - нуль n-того порядка.
Заметим, что в
нуле n-того порядка f(z0)=f'(z0)=…
f(n-1)(z0)=0, f(n)(z0) 0 и
f(z)=(z-z0)n f1(z),
f1(z0)
0 и
f(z)=(z-z0)n f1(z),
f1(z0) 0.
0.
Теорема о нулях
аналитической функции.
Пусть f(z) C
C (g) и обращается в 0 в бесконечном множестве различных
точек
(g) и обращается в 0 в бесконечном множестве различных
точек
(z i zk ,
все z n
zk ,
все z n g и f(z n )=0), имеющем предельную точку (точку сгущения) z
*
g и f(z n )=0), имеющем предельную точку (точку сгущения) z
* g
g
( zn=z*
zn=z* g).
Тогда f(z)
g).
Тогда f(z) 0, для z
0, для z g.
g.
Доказательство. По непрерывности
f(z*)=0 => f(z)= cn(z-z*)n
, где |z-z *|< r (z*) => c0 =0, и f(z)=(z-z *)f1(z);
f1(z)=
cn(z-z*)n
, где |z-z *|< r (z*) => c0 =0, и f(z)=(z-z *)f1(z);
f1(z)=  cn(z-z*)n; f1(zn
)=0=> по непрерывности f
1(z*)=0 => c1 =0 и так далее => c n =0 для " n. Итак f(z)
cn(z-z*)n; f1(zn
)=0=> по непрерывности f
1(z*)=0 => c1 =0 и так далее => c n =0 для " n. Итак f(z) 0
в круге |z-z *| < r (z*
), где r
(z* ) не меньше, чем расстояние
от z * до
0
в круге |z-z *| < r (z*
), где r
(z* ) не меньше, чем расстояние
от z * до 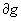 . Тождественное равенство f(z)
. Тождественное равенство f(z) 0 во всей области g доказывается
аналогично доказательству принципа максимума
0 во всей области g доказывается
аналогично доказательству принципа максимума
Достаточно показать, что f(z
** )=0, где z ** g -
произвольная точка, лежащая вне круга |z-z *| <
r (z* ).
Соединим z * и z **
спрямляемой кривой L, целиком лежащей в g и
отстоящей от
g -
произвольная точка, лежащая вне круга |z-z *| <
r (z* ).
Соединим z * и z **
спрямляемой кривой L, целиком лежащей в g и
отстоящей от 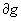 на
расстояние d>0. Поскольку " точку круга |z-z *|< r (z* ), лежащую
внутри g можно рассматривать как предел последовательности нулей функции f(z),
то выбрав в качестве нового центра разложения последнюю точку z=z
1 пересечения кривой L с
окружностью |z-z *|= r (z*
), получим, что f(z)
на
расстояние d>0. Поскольку " точку круга |z-z *|< r (z* ), лежащую
внутри g можно рассматривать как предел последовательности нулей функции f(z),
то выбрав в качестве нового центра разложения последнюю точку z=z
1 пересечения кривой L с
окружностью |z-z *|= r (z*
), получим, что f(z) 0 внутри круга |z-z 1|< r (z1 ), где
0 внутри круга |z-z 1|< r (z1 ), где
r (z1) d. Продолжая этот
процесс, покроем кривую L конечным числом кругов, радиусов не меньше d, внутри
которых f(z)
d. Продолжая этот
процесс, покроем кривую L конечным числом кругов, радиусов не меньше d, внутри
которых f(z) 0. При этом точка z=z
** попадет внутрь последнего
круга => f(z **)
0. При этом точка z=z
** попадет внутрь последнего
круга => f(z **) 0. В силу произвольности z **
=> f(z)
0. В силу произвольности z **
=> f(z) 0 в g. n
0 в g. n
Следствия.
1. Все нули
f(z) C
C (g) и f(z)
тождественно
(g) и f(z)
тождественно  0 в g -
изолированные.
0 в g -
изолированные.
2. Если
f(z) C
C (g) и
f(z) тождественно
(g) и
f(z) тождественно  0 в g, то в
" ограниченной
0 в g, то в
" ограниченной 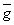 '
' g может быть лишь конечное число нулей
f(z).
g может быть лишь конечное число нулей
f(z).
Доказательство Если
множество нулей в 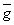 '- бесконечно, то из него можно выделить пооследовательность,
сходящуюся к z
'- бесконечно, то из него можно выделить пооследовательность,
сходящуюся к z
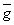 ' =>f(z)
' =>f(z) 0 в g, что
противоречит условию. n
0 в g, что
противоречит условию. n
2. Если f(z)- целая , то в "
ограниченной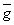 '
может быть лишь конечное число нулей f(z). На расширенной комплексной плоскости целая функция может иметь лишь счетное число нулей,
причем предельноой точкой этого множества является бесконечно удаленная точка .
'
может быть лишь конечное число нулей f(z). На расширенной комплексной плоскости целая функция может иметь лишь счетное число нулей,
причем предельноой точкой этого множества является бесконечно удаленная точка .
3. Теорема единственности
определенной аналитической функции.
Теорема.
Если f1 (z) и f
2(z) C
C (g) и $
{zn}
(g) и $
{zn}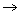 z*
z* g, zi
g, zi zk и f
1(zn)=f2(zn ), то f 1(z)
zk и f
1(zn)=f2(zn ), то f 1(z) f2 (z) для
" z
f2 (z) для
" z g.
g.
Для доказательства достаточно при
помощи теоремы о нулях установить, что функция h(z)=f
1(z)-f2(z) 0 в g.
0 в g.
Следствия теоремы единственности.
Множество задания аналитической функции.
В области g может существовать
только одна аналитическая функция, принимающая заданные значения на
a) {zn}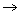 z*
z* g, zi
g, zi zk
zk
b ) x C
C g, C- кусочно-гладкая кривая.
g, C- кусочно-гладкая кривая.
c) z
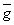 '
' g.
g.
Другими словами: Функция аналитическая в g
однозначно определяется заданием своих значений
на a), b), c).
Существенное замечание. Может - не значит
существует. Нельзя произвольно задавать значения f(z n ) или f(C) или f(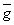 ') !
') !