Лекция 9.
- §15. Ряд Лорана.
- 1. Кольцо сходимости ряда Лорана.
- 2. Теорема о разложении функции
комплексной переменной, аналитической в круговом кольце в ряд Лорана.
1. Кольцо сходимости ряда
Лорана.
 cn(z-z0)n=
cn(z-z0)n= cn(z-z0)n+
cn(z-z0)n+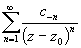 =P(z)+Q(z). P(z) называется правильной частью ряда
Лорана, Q(z)- главной частью ряда Лорана. P(z)
=P(z)+Q(z). P(z) называется правильной частью ряда
Лорана, Q(z)- главной частью ряда Лорана. P(z) C
C (|z-z0|<R1).
(|z-z0|<R1).
В
какой области Q(z) будет аналитической функцией? Сделаем замену
1/(z-z0)= x ;
Q(z)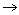 Q(
x )=
Q(
x )= c-n
x n
c-n
x n C
C (| x
|<1/R2 ), где мы обозначили
через 1/R 2 радиус сходимости
полученного степенного ряда. При R 2<R1 существует общая область сходимости- круговое
кольцо R2<|z-z0|<R1.
(| x
|<1/R2 ), где мы обозначили
через 1/R 2 радиус сходимости
полученного степенного ряда. При R 2<R1 существует общая область сходимости- круговое
кольцо R2<|z-z0|<R1.
Следствия теоремы Абеля :
1.  cn(z-z0)n
cn(z-z0)n C
C (R2<|z-z0|<R1).
(R2<|z-z0|<R1).
2. Внутри кругового кольца сходимости
ряд Лорана можно почленно дифференцировать и интегрировать любое число раз, при
этом полученные ряды также  C
C (R2<|z-z0|<R1).
(R2<|z-z0|<R1).
3.
R1 определяется через {c
n}, n=0,..., :
R1=1/L1, L1=
:
R1=1/L1, L1= или L
1=
или L
1= , а R 2 -через {c -n}, n=1,...,
, а R 2 -через {c -n}, n=1,..., : R2=
: R2= , или
R 2=
, или
R 2=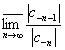 .
.
4. Коэффициенты ряда
Лорана c n через значения суммы
ряда в точке z 0 не
определяются! В точке z 0 сумма
ряда Лорана не определена!
2. Теорема о разложении функции комплексной
переменной, аналитической в круговом кольце в ряд Лорана.
Т еорема 15.1 Если
f(z) C
C (R2<|z-z0|<R1
), то она однозначно разложима в этом кольце в ряд
Лорана f(z)=
(R2<|z-z0|<R1
), то она однозначно разложима в этом кольце в ряд
Лорана f(z)= cn(z-z0)n.
cn(z-z0)n.
Доказательство. Фиксируем произвольную точку z
внутри кольца : (R2<|z-z0|<R1 ) и построим окружности C' 1 : | x -z0|=R'1 и C' 2: : | x
-z0|=R'2 , с центром в
точке z 0 и радиусами R'
1 и R' 2 :
R2<R'2<|z-z0|<R'1<R1
. По формуле Коши для многосвязной области
f(z)=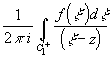 +
+  =P(z)+Q(z).
=P(z)+Q(z).
На окружности C' 1: | x -z0|=R’1 выполняется неравенство  . Поэтому, дробь 1/( x -z) можно представить в виде
. Поэтому, дробь 1/( x -z) можно представить в виде
1/( x -z)=1/[( x
-z0)-(z-z0)]= и
проведя почленное интегрирование, что возможно в силу равномерной сходимости
ряда по переменной x на C R (см. доказательство теоремы Тейлора) получим P(z)=
и
проведя почленное интегрирование, что возможно в силу равномерной сходимости
ряда по переменной x на C R (см. доказательство теоремы Тейлора) получим P(z)= cn(z-z0)n ,
где
cn(z-z0)n ,
где
c n= , n
, n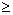 0.
0.
На окружности C' 2: | x -z0|=R’2 выполняется неравенство 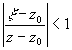 . Поэтому, дробь
. Поэтому, дробь
1/( x -z) можно представить в виде 1/( x -z)=1/[( x
-z0)-(z-z0)]=
=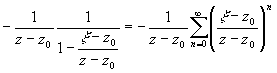 В
результате почленного интегрирования этого ряда получим: Q(z)=
В
результате почленного интегрирования этого ряда получим: Q(z)=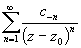 ,
n>0, где c -n=-
,
n>0, где c -n=-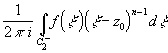 .
Изменив направление интегрирования, получим: c -n=
.
Изменив направление интегрирования, получим: c -n=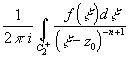 ,
n>0. Подынтегральные функции в выражениях для c n и c -n являются аналитическими в круговом кольце R
2<|z-z0|<R1. Поэтому в силу теоремы Коши значения соответствующих интегралов не изменится при
произвольной деформации контуров интегрирования в области аналитичности
подынтегральных функций. Это позволяет записать общее выражение c
n=
,
n>0. Подынтегральные функции в выражениях для c n и c -n являются аналитическими в круговом кольце R
2<|z-z0|<R1. Поэтому в силу теоремы Коши значения соответствующих интегралов не изменится при
произвольной деформации контуров интегрирования в области аналитичности
подынтегральных функций. Это позволяет записать общее выражение c
n= , n=0, ± 1, ± 2,…,
где C- произвольный замкнутый контур, лежащий в
кольце R 2<|z-z0|<R1 и содержащий точку z 0 внутри. Для f(z) окончательно можно записать:
f(z)=
, n=0, ± 1, ± 2,…,
где C- произвольный замкнутый контур, лежащий в
кольце R 2<|z-z0|<R1 и содержащий точку z 0 внутри. Для f(z) окончательно можно записать:
f(z)= cn(z-z0)n+
cn(z-z0)n+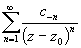 =
= cn(z-z0)n
, где c n=
cn(z-z0)n
, где c n= .
.
Т.к. z-произвольная точка внутри кольца
R 2<|z-z0|<R1 => ряд  cn(z-z0)n сходится к f(z) всюду внутри данного кольца, причем в
замкнутом кольце R2<R'2
cn(z-z0)n сходится к f(z) всюду внутри данного кольца, причем в
замкнутом кольце R2<R'2 |z-z0|
|z-z0| R'1<R1 ряд сходится к f(z) равномерно
.
R'1<R1 ряд сходится к f(z) равномерно
.
Докажем единственность. Предположим,
что имеет место другое разложение f(z)=  c'n(z-z0)n , где хотя бы один коэффициент c' n
c'n(z-z0)n , где хотя бы один коэффициент c' n cn . Тогда всюду внутри кольца R
2<|z-z0|<R1 имеет место равенство:
cn . Тогда всюду внутри кольца R
2<|z-z0|<R1 имеет место равенство:  c'n(z-z0)n=
c'n(z-z0)n= c'n(z-z0)n
. Проведем окружность C R , радиуса R, R 2<R<R1
, с центром в точке z 0 . Тогда ряды
c'n(z-z0)n
. Проведем окружность C R , радиуса R, R 2<R<R1
, с центром в точке z 0 . Тогда ряды  c'n(z-z0)n и
c'n(z-z0)n и  c'n(z-z0)n сходятся на C R равномерно. Умножим оба ряда на (z-z
0)-m-1 , где m-
произвольное целое число и проинтегрируем почленно. Рассмотрим
c'n(z-z0)n сходятся на C R равномерно. Умножим оба ряда на (z-z
0)-m-1 , где m-
произвольное целое число и проинтегрируем почленно. Рассмотрим  . Положив z-z
0=Rei j ., получим
. Положив z-z
0=Rei j ., получим 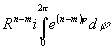 =
=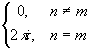 .=>
для произвольного целого m c' m=cm
. n
.=>
для произвольного целого m c' m=cm
. n
Точной областью сходимости ряда Лорана является круговое
кольцо R2<|z-z0|<R1 , на границах
которого имеется хотя бы по одной особой точке аналитической функции f(z), к
которой (к функции) сходится данный ряд. (см.
Теорему 13.1)
 , а R 2 -через {c -n}, n=1,...,
, а R 2 -через {c -n}, n=1,...,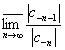 .
.
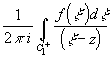 +
+  =P(z)+Q(z).
=P(z)+Q(z). . Поэтому, дробь 1/( x -z) можно представить в виде
. Поэтому, дробь 1/( x -z) можно представить в виде
 и
проведя почленное интегрирование, что возможно в силу равномерной сходимости
ряда по переменной x на C R (см. доказательство теоремы Тейлора) получим P(z)=
и
проведя почленное интегрирование, что возможно в силу равномерной сходимости
ряда по переменной x на C R (см. доказательство теоремы Тейлора) получим P(z)= , n
, n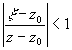 . Поэтому, дробь
. Поэтому, дробь 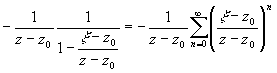 В
результате почленного интегрирования этого ряда получим: Q(z)=
В
результате почленного интегрирования этого ряда получим: Q(z)=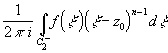 .
Изменив направление интегрирования, получим: c -n=
.
Изменив направление интегрирования, получим: c -n=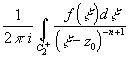 ,
n>0. Подынтегральные функции в выражениях для c n и c -n являются аналитическими в круговом кольце R
2<|z-z0|<R1. Поэтому в силу теоремы Коши значения соответствующих интегралов не изменится при
произвольной деформации контуров интегрирования в области аналитичности
подынтегральных функций. Это позволяет записать общее выражение c
n=
,
n>0. Подынтегральные функции в выражениях для c n и c -n являются аналитическими в круговом кольце R
2<|z-z0|<R1. Поэтому в силу теоремы Коши значения соответствующих интегралов не изменится при
произвольной деформации контуров интегрирования в области аналитичности
подынтегральных функций. Это позволяет записать общее выражение c
n= , n=0, ± 1, ± 2,…,
где C- произвольный замкнутый контур, лежащий в
кольце R 2<|z-z0|<R1 и содержащий точку z 0 внутри. Для f(z) окончательно можно записать:
f(z)=
, n=0, ± 1, ± 2,…,
где C- произвольный замкнутый контур, лежащий в
кольце R 2<|z-z0|<R1 и содержащий точку z 0 внутри. Для f(z) окончательно можно записать:
f(z)= .
.
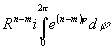 =
=